九年级（上）月考数学试卷

九年级（上）月考数学试卷

参考公式：二次函数y=ax²+bx+c的顶点坐标是

一. 选择题（本题共10小题，每小题4分，共40分）

1．下列函数中，y与x成反比例的是　　　　　　　　　　　　　　　　　　 （　　　）

　 A、　　　　 B、　　　 C、　　 D、

2.下列各点在反比例函数图象上的是　　　　　　　　　　　　　　 （　　　）

A、（1，4）　　 B、（2，-2）　　 C、（2，2）　　　 D、（，-1）

3．反比例函数的图象大致是　　　　　　　　　　　　　　　　　  （　　　）

A 　　　　　　　　 B 　　　　　　　 C　　　　　　　　　 D

4、如图，点C在⊙O上，已知∠C＝50°，则∠AOB为　　　　　　　　　　  （　　　）

A、50°　　　　　　　　 B、25°

C、100°　　　　　　　　D、65°

5．两条抛物线 和，在同一坐标系内，下列说法不正确的是　（　　　）

A、顶点坐标相同　　　　 　　B、对称轴相同

C、开口方向相反　　 　　　　D、都有最低点

6．已知，则下列关系式中错误的是　　　　　　　　　　　　　　　 （　　　）

 A、 　 B、　　 C、　　　 D、

7．抛物线与x轴的交点个数为　　　　　　 　　　　　　　　 （　　  ）

 A、0个　　　　　B、1个　　　　 C、2个　　　　　 D、不能确定

8．在比例尺为1：10的图纸上，某矩形零件的面积为12cm²，则零件实际面积为（　 ）

A、12cm² 　　　　 B、120cm² 　　　C、1200cm² 　　　 D、1.2cm²

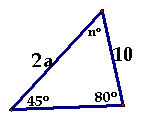
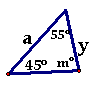9．已知如图两个三角形，则y、m、n的值分别为（　 ）

A、5，80，55　　　　 B、5，55，80 　　

C、10，80，55  　　　D、5，100，80

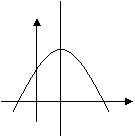10、二次函数的图象如图所示，则下列结论中正确的是： （　　 ）

　 A　a>0　b<0　c>0　　　B　a<0　b<0　c>0

  C　a<0　b>0　c<0　　　

D　a<0　b>0　c>0

　　

二、填空题（本题有6小题，每小题5分，共30分）　

11、抛物线y＝(x－2)²＋3的顶点坐标是_________

12.将抛物线y=2x² -3 向上平移2个单位，所得抛物线表达式为______

13．如图，ＡＢ是⊙O的直径，能用图中字母表示出的劣弧是______，

优弧是______．(各写出一条即可)

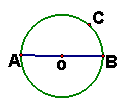
　　　　  　 (第13题图)　　　　　　　　　　　　　　　　  (第15题图)

14．线段a=2，b=8，则线段a，b的比例中项是______.

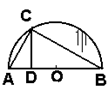
15、如图，AB是半圆O的直径，过⊙O上一点C,作CD⊥AB于点D ，

请找出一个与 △ABC相似的三角形:_______

16．反比例函数，当时， 与的大小关系为______.

三、解答题（本题有8小题 ，共80分）

17. （ 10分)若一个面积为16cm²的矩形的宽y（cm），长x（cm）。

（1）写出y与x的函数关系式，以及自变量x的取值范围。

（2）在右方格中用描点法画出所求函数的图象。

 

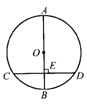
18、（8分) 如图，AB是⊙O的直径，AB⊥CD, AB=10,CD=8, 求AE的长.

 

19.（8分) 已知如图:AB,DE是⊙O的直径,C是⊙O上一点, 且AD=CE,

求证:  BE=CE.

20．(8分) 已知,求的值.

21（12分) 已知二次函数图象经过点（１，-２），（０，－１），（－１，－４）

　　（１）求此函数解析式；

（２）求此函数的最大值．

22. （ 10分)已知扇形的圆心角为150⁰,半径为2,求这个扇形的弧长与面积.

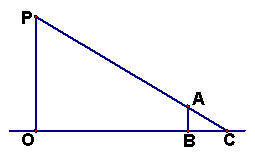
23．（ 10分) 如图，一天晚上，李杨在广场上乘凉. 图中线段AB表示站在广场上的李杨，线段PO表示直立在广场上的灯杆，点P表示照明灯, BC表示李杨在照明灯 P 照射下的影子。如果灯杆高PO=12m，李杨的身高AB=1.6m，李杨与灯杆的距离BO=13m，请求出李杨影子的长度.

24．（ 14分)某电影院有1000个座位，门票每张３元，可达客满；根据市场统计，若每张门票提高1元，将有200 张门票不能售出．

　　（１）若每张门票提高ｘ元，将有­­______________张门票不能售出(用x的代数式表示)；

(2)求提价后每场电影的票房收入ｙ（元）与票价提高量ｘ（元）之间的函数关系及自变量ｘ的取值范围；

（3）为增加收入，电影院应做怎样的决策（提价还是降价？若提价，提价多少为宜？）