中考数学试题1
分
类
荟
萃
之
四
边
形
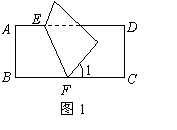1、如图1，把矩形
沿
对折，若
，则
等于（ ）（广东梅州）
Ａ．
Ｂ．
Ｃ．
Ｄ．
2、用两个全等的正方形和
拼成一个矩形
，把一个足够大的直角三角尺的直角顶点与这个矩形的边
的中点
重合，且将直角三角尺绕点按逆时针方向旋转．
（1）当直角三角尺的两直角边分别与矩形的两边
相交于点
时，如图
甲，通过观察或测量
与
的长度，你能得到什么结论？并证明你的结论．
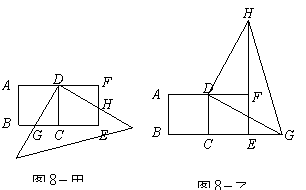（2）当直角三角尺的两直角边分别与
的延长线，的延长线相交于点时（如图乙），你在图甲中得到的结论还成立吗？简要说明理由．（广东梅州）
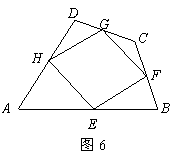
3、．如图6，点
分别为四边形的边
的中点，试判断四边形
的形状，并证明你的结论．(广东湛江)
 |
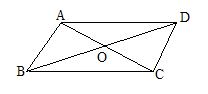4、．如图所示，在□ABCD中，对角线AC、BD交于点O，下列式子中一定成立的是 ( ) （广东）
A．AC⊥BD B．OA=0C
C．AC=BD D．A0=OD
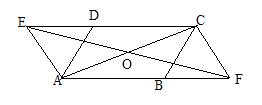5、如图，在□ABCD中，∠DAB=60°，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．
(1)求证：四边形AFCE是平行四边形．
(2)若去掉已知条件的“∠DAB=60°，上述的结论还成立吗?若成立，请写出证明过程；
若不成立，请说明理由．（广东）
6、如图所示，在平面直角坐标中，四边形OABC是等腰梯形，BC∥OA，OA=7，AB=4，∠ COA=60°，点P为x轴上的—个动点，点P不与点0、点A重合．连结CP，过点P作PD交AB于点D．
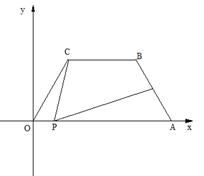(1)求点B的坐标；
(2)当点P运动什么位置时，△OCP为等腰三角形，求这时点P的坐标；
(3)当点P运动什么位置时，使得∠CPD=∠OAB，且
=
，求这时点P的坐标。（广东）
7、顺次连结矩形的各边中点，所得的四边形一定是（ ）（广东肇庆）
Ａ．正方形 Ｂ．菱形 Ｃ．矩形 Ｄ．梯形
8、下列正多边形中，与正三角形同时使用，能进行密铺的是（ ）（广东肇庆）
Ａ．正十二边形 Ｂ．正十边形 Ｃ．正八边形 Ｄ．正五边形
9、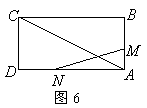
如图6，已知矩形的边长
．某一时刻，动点
从
点出发沿
方向以
的速度向
点匀速运动；同时，动点
从点出发沿
方向以
的速度向点匀速运动，问：
（1）经过多少时间，
的面积等于矩形面积的
？
（2）是否存在时刻
，使以
为顶点的三角形与
相似？若存在，求的值；若不存在，请说明理由．
（广东肇庆）
10、如图3一①，将一块正方形木板用虚线划分成36个全等的小正方形，然后，按其中的
实线切成七块形状不完全相同的小木片，制成一副七巧板．用这副七巧板拼成图3一②
的图案，则图3一②中阴影部分的面积是整个图案面积的( )．（广州）
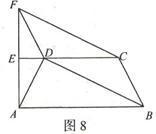
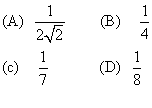
11、图8是某区部分街道示意图，其中CE垂直平分AF，
AB／／DC，BC／／DF．从B站乘车到E站只有两条路线有直
接到达的公交车，路线1是B---D---A---E，路线2是
B---C---F---E，请比较两条路线路程的长短，并给出证明．
（广州）
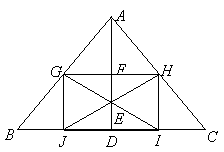
12、如图，在
中，
，
是高
上的动点，
是点关于点的对称点（点在高上，且不与，重合）．过点作
的平行线与交于
，与
交于
，连结
并延长交于点
，连结
并延长交于点
，连结
，
．
（1）求证：四边形
是矩形；
（2）若
，
，设
，
．
①求
与
的函数关系式，并写出自变量的取值范围；
②点在何处时，矩形的面积与
的面积相等？
（广东韶关）
13、如图，在平行四边形ABCD中，AC、BD相交于点O，下列结论：①OA＝OC；②∠BAD＝∠BCD；③AC⊥BD；④∠BAD＋∠ABC＝180°中，正确的个数有（ ）。
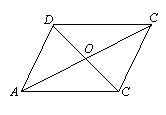A、1个 B、2个
C、3个
D、4个
（广东佛山）
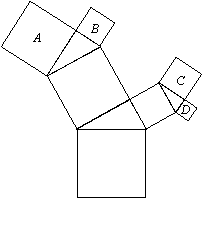14、如图，所有的四边形都是正方形，所有三角形都是直角三角形，其中最大的正方形的边长是a，则图中四个小正方形A、B、C、D的面积之和是
。
（广东佛山）
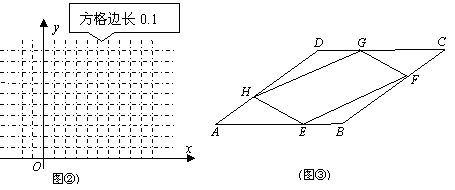
15、已知：在四边形ABCD中，AB＝1，E、F、G、H分别时AB、BC、CD、DA上的点，且AE＝BF＝CG＝DH。设四边形EFGH的面积为S，AE＝x(0≤x≤1)。
(1)如图①，当四边形ABCD为正方形时，
<1>求S关于x的函数解析式，并求S的最小值S0；
<2>在图②中画出<1>中函数的草图，并估计S＝0.6时x的近似值(精确到0.01)；
(2)如图③，当四边形ABCD为菱形，且∠A＝30°时，四边形EFGH的面积是否存在最小值？若存在，求出最小值；若不存在，请说明理由。（广东佛山）
 | |||
 | |||
16、