中考数学试题分类
荟
萃
之
基
本
图
形
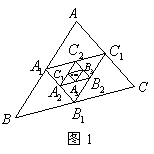1.如图1，已知
的周长为
，分别连接的中点
得
，再连接
的中点
得
，再连接
的中点
得
，这样延续下去，最后得
．
设的周长为
，的周长为
，
的周长为
， 的周长为
，则
．(06广东梅州)
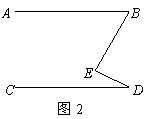
2. 如图2，已知直线
，
，
，
则
度．(06广东湛江)
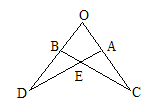
3. 如图，若△OAD≌△OBC，且∠0=65°，∠C=20°，
则∠OAD= ．(06珠海)
 |
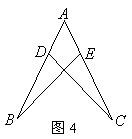4. 如图4，已知
．
（1）求证：
；
（2）若
，问
经过怎样的变换能与
重合？
(06广东肇庆)
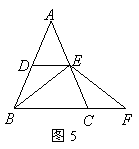5. 在中，
，点
分别是
的中点，
是
延长线上的一点，且
．
（1）求证：
；
（2）求证：
．(06广东肇庆)
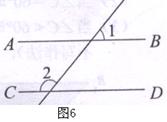
6. 如图1，AB／／CD，若∠2=135°，则么∠l的度数是( )．(06广州)
(A)30° (B)45° (C)60° (D)75°
7. 已知四组线段的长分别如下，以各组线段为边，能组成三角形的是( )．(06广州)
(A)l，2，3 (B)2，5，8 (C)3，4，5 (D)4，5，10
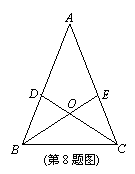8.. 如图，D、E分别为△ABC的边AB、AC上的点，BE与CD相交于O点。现有四个条件：①AB＝AC；②OB＝OC；③∠ABE＝∠ACD；④BE＝CD。
(1)请你选出两个条件作为题设，余下的两个作为结论，写出一个正确的命题：
命题的条件是 和 ，命题的结论是 和 (均填序号)。
(2)证明你写出的命题。
已知：
求证：
证明：
(06广东佛山)
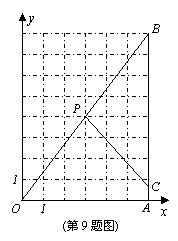9. 已知：Rt△OAB在直角坐标系中的位置如图所示，P(3，4)为OB的中点，点C为折线OAB上的动点，线段PC把Rt△OAB分割成两部分。
问：点C在什么位置时，分割得到的三角形与Rt△OAB相似？(注：在图上画出所有符合要求的线段PC，并求出相应的点C的坐标)。
(06广东佛山)
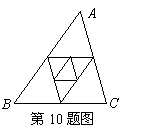10. 如右图，已知的周长为
，连结三边的中点构成第二个三角形，再连结第二个三角形三边的中点构成第三个三角形，
，依此类推，则第10个三角形的周长为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
(06广东韶关)
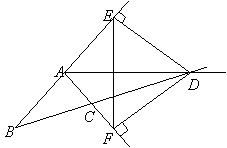11. 如图，在中，
，
的外角平分线交直线于
，过作
，
分别交直线
，
于
，，连结
．
（1）求证：
；
（2）若
，且
，求
的长．
(06广东韶关)
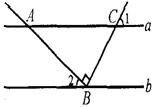
12. 如图，直线a／／b，点B在直线b上，且AB ⊥BC ,∠1 二 55 º ，则∠2 的度数为 ( ) (06安徽)
A . 35 º B . 45 º C . 55 º D . 125º
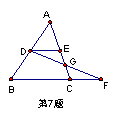
13. 如图，在△ABC中，D、E分别是AB和AC的中点，F是BC延长线上的一
点，DF平分CE于点G，
，则
，△ADE与△ABC的周
长之比为 ，△CFG与△BFD的面积之比为 。(06常州)
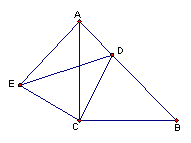14. 已知：如图，△ABC和△ECD都是等腰直角三角形，
，D为AB边上一点，
求证：（1）△ACE≌△BCD；（2）
(06常州)
15. 已知：如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，求证：AF=DE。
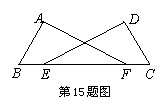(06福建三明)
16. 在如图12－1至图12－3中，△ABC的面积为a ．
（1）如图12－1, 延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S1，则S1=________（用含a的代数式表示）；
（2）如图12－2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S2，则S2=__________（用含a的代数式表示），并写出理由；
（3）在图12－2的基础上延长AB到点F，使BF=AB，连结FD，
FE，得到△DEF（如图12－3）．若阴影部分的面积为S3，
则S3=__________（用含a的代数式表示）．
发现
像上面那样，将△ABC各边均顺次延长一倍，连结所得端点，得到△DEF（如图12－3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的_______倍．
应用
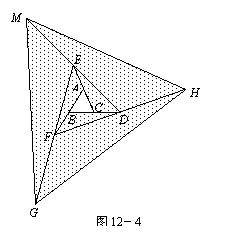
去年在面积为10m2的△ABC空地上栽种了某种花卉．今年准备扩大种植规模，把△ABC向外进行两次扩展，第一次由△ABC扩展成△DEF，第二次由△DEF扩展成△MGH（如图12－4）．求这两次扩展的区域（即阴影部分）面积共为多少m2？(06河北)
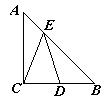
17. 如图，在△ABC中，AC=BC=2,∠ACB=90º,D是BC边的中点，E是AB边上一动点，则EC+ED的最小值是_______________．
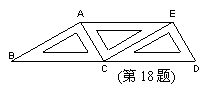
18. 如图，将三个相同的三角尺不重叠不留空隙地拼在一起，观察图形，在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有（ ）.
（A）4组 （B）3组 （C）2组 （D）1组(06湖北宜昌)
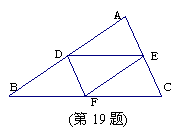
19．如图19,在△ABC 中，D、E、F分别是AB、AC、BC的中点 ,则△DEF与△ABC的周长之比为( ). (06湖北宜昌)
（A）1:
（B）1:2 （C）1:3 （D）1:4
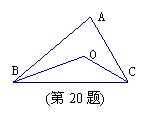
21. 如图，在△ABC中,点O是∠ABC与∠ACB平分线的交点，
若∠BAC=80o,则∠BOC＝( ).
(A)130o (B)100o (C)50o (D)65o
(06湖北宜昌)
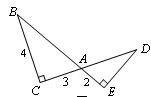
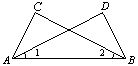
22. 如图，∠C＝∠E＝90°，AC＝3，BC＝4，AE＝2，则AD＝________．(06浙江嘉兴)
 |
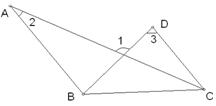
23. 如图，已知∠1＝∠2，∠C＝∠D，求证：AC＝BD．
(06浙江嘉兴)
24. 如图，已知AB∥CD。则 ( ) (06临沂)
A．∠1＝∠2＋∠3 B．∠1＝2∠2＋∠3
C．∠1＝2∠2－∠3 D．∠1＝180º－∠2－∠3
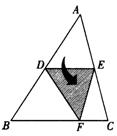
25. 如图，D、E为AB、AC的中点，将△ABC沿线段DE折叠，使点A落
在点F处，若∠B=500，则∠BDF= .(06山东枣庄)
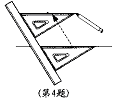
26. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是 ( ) (06苏州)
A．同位角相等，两直线平行
B．内错角相等，两直线平行
C．同旁内角互补，两直线平行
D．两直线平行，同位角相等
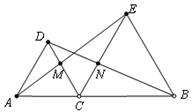
27. 如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：① △ACE≌△DCB； ② CM＝CN；③ AC＝DN。其中，正确结论的个数是 ( ) （06天津）
(A) 3个 （B）2个
(C) 1个 （D）0个
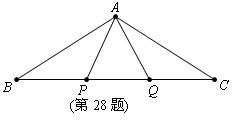
28. 如图，P，Q是△ABC的边BC上的两点，且BP＝PQ＝QC＝AP＝AQ，则∠ABC的大小等于____________（度）（06天津）
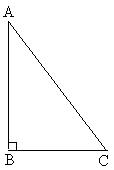
29. 已知Rt△ABC中，∠C=90º。
（1）根据要求作图（尺规作图，保留作图痕迹，不写画法）
①作∠BAC的平分线AD交BC于D；
②作线段AD的垂直平分线交AB于E，交AC于F，垂足为H；
③连接ED。
（2）在（1）的基础上写出一对相似比不为1的相似三角形和一对全等三角形：
△________∽△________；△________≌△________。
并选择其中一对加以证明。(06浙江湖州)
证明：
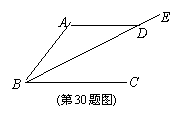
30. 如图，AD∥BC，点E在BD的延长线上，若∠ADE=155°，则∠DBC的度数为
A、155° B、50° C、45° D、25°(06北京课标)
31.
如图，在△ABC中，AB=AC，M、N分别是AB、AC的中点，D、E为BC上
的点，连结DN、EM。若AB=13cm，BC=10cm，DE=5cm，则图中阴影部分的面
积为__________cm2。(06北京课标)
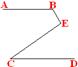32. 如图, AB//CD, 若∠ABE=1200,
∠DCE=350, 则有∠BEC=__________度.
(06广安)
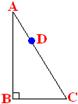
33. 如图, Rt△ABC, 斜边AC上有一动点D(不与点A、C重合), 过D点作直线截△ABC, 使截得的三角形与△ABC相似, 则满足这样条件的直线共有________条.
(06广安)
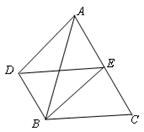
34. 如图，DB∥AC，且DB=
AC，E是AC的中点，求证：BC=DE。(06湖北黄冈)
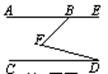
35. 如图,直线AE∥CD,∠EBF=135°,∠BFD=60°,则∠D等于( )
(A)75°. (B)45°. (C)30°. (D)15°.（06湖北荆门）
36．下列图中能够说明
的是（ ）
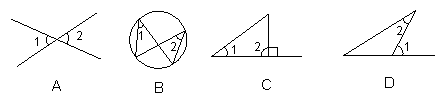
37. E、F分别是平行四边形ABCD的边BA、DC延长线上的点，且AE=CF，EF交AD于G，交BC于H。
（1）图中的全等三角形有 对，它们分别是 ；（不添加任何辅助线）
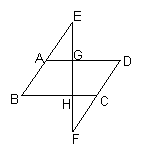（2）请在（1）问中选出一对你认为全等的三角形进行证明。
我选择的是： 。(06四川乐山)
证明：
38. 已知等腰
的腰AB＝AC＝10cm，，底边BC=12cm,则
的平分线的长是
cm.(06攀枝花)
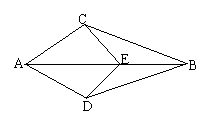39. 点E在AB上，AC=AD，请你添加一个条件，使图中存在全等三角形，并给予证明。
所添条件为 ，
你得到的一对全等三角形是
(06攀枝花)
证明：
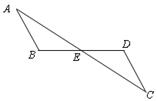40. AC和BD相交于点E，AB∥CD，BE=DE。求证：AB=CD
（06武汉）
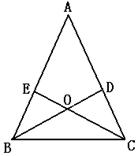41. 如图, △ABC中, D、E分别是AC、AB上的点, BD与CE交于点O. 给出下列三个条件：
①∠EBO＝∠DCO；②∠BEO＝∠CDO；③BE＝CD.
⑴ 上述三个条件中, 哪两个条件可判定△ABC是等腰三角形(用序号写出所有情形)；
⑵ 选择第⑴小题中的一种情形, 证明△ABC是等腰三角形.
(06扬州)
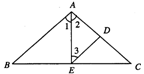42. 如图，在钝角△ABC中，点D、E分别是边AC、BC
的中点，且DA＝DE，那么下列结论错误的是（ ）
A.∠1=∠2 B.∠1=∠3
C.∠B=∠C D.∠B=∠C （06云南）
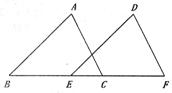43. 已知：如图，AB//DE，且AB=DE.
(l）请你只添加一个条件，使△ABC≌△DEF,
你添加的条件是 .
(2）添加条件后，证明△ABC≌△DEF.
（06云南）
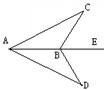
44. 如图，点B在AE上，∠CAB=∠DAB，要使△ABC≌△ABD，
可补充的一个条件是： _________ （写一个即可）．
（06浙江）