中考数学最新题型精选（二）
1、如图1，将矩形沿对称轴折叠，在对称轴处剪下一块，余下部分的展开图为（ ）
|
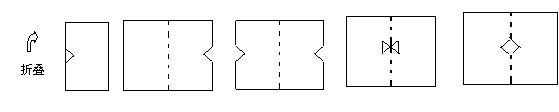
A B C D
2、2006年2月23日《日报》公布了2000年~2005年某市城市居民人均可支配收入情况（如图所示）
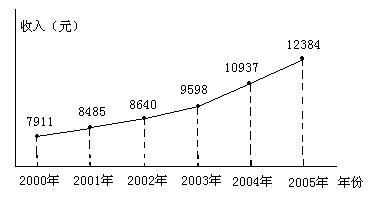
根据图示信息：
(1)求某市城市居民人均可支配收入的中位数；
(2)哪些年份某市城市居民人均可支配收入比上一年增加了1000元以上？
(3)如果从2006年开始，某市城市居民人均可支配收入每一年比上一年增加a 元，那么到2008年底可达到18000元，求a的值．
3、下列四幅图形中，表示两颗小树在同一时刻阳光下的影子的图形可能是( )
A. B. C. D.
4、如图，点M是直线y＝2
＋3上的动点，过点M作MN垂直于轴于点N，
轴上是否存在点P，使△MNP为等腰直角三角形.小明发现：当动点M运动到（－1，1）时，y轴上存在点P（0，1）,此时有MN=MP，能使△NMP为等腰直角三角形.那么，在y轴和直线上是否还存在符合条件的点P和点M呢？请你写出其它符合条件的点P的坐标 ．
5、现有9个相同的小正三角形拼成的大正三角形,将其部分涂黑.如图(1),(2)所示.
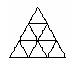
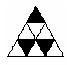
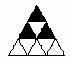
图(1) 图(2) 图(3) 图(4)
观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形②涂黑部分都是三个小正三角形.
请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征．
6、初三(1)班数学兴趣小组在社会实践活动中，进行了如下的课题研究：用一定长度的铝合金材料,将它设计成外观为长方形的三种框架，使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:
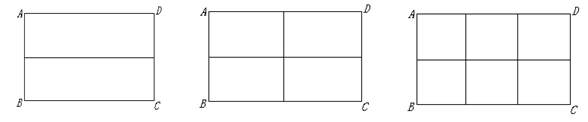
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,
长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为m,长方形框架ABCD的面积为Ｓ＝ (用含的代数式表示)；当AB＝
m时, 长方形框架ABCD的面积Ｓ最大;
在图案(3)中,如果铝合金材料总长度为
m, 设AB为m,当AB=
m时, 长方形框架ABCD的面积Ｓ最大.
(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律． …
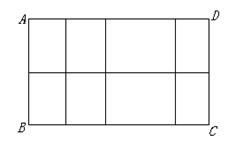探索: 如图案(4),如果铝合金材料总长度为
m共有ｎ条竖档时, 那么当竖档AB多少时,长方形框架ABCD的面积最大.
图案(4)
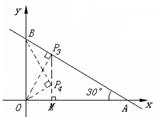
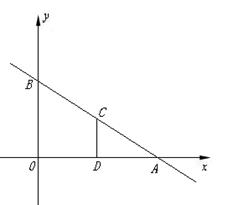7、如图,平面直角坐标系中,直线AB与轴,轴分别交于A(3,0),B(0,
)两点, ,点C为线段AB上的一动点,过点C作CD⊥轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD＝
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
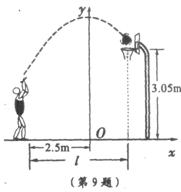
8、小敏在某次投篮中，球的运动路线是抛物线y=-
x2+3.5的一部分(如图)，若命中篮圈中心，则他与篮底的距离l是(
)
A．3.5m
B．4m
C．4.5m
D．4.6m
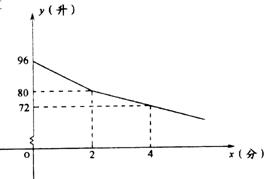
9、某校部分住校生，放学后到学校锅炉房打水，每人接水2升，他们先同时打开两个放水笼头，后来因故障关闭一个放水笼头．假设前后两人接水间隔时间忽略不计，且不发生泼洒，锅炉内的余水量y(升)与接水时间x(分)的函数图象如图．
请结合图象，回答下列问题：
(1)根据图中信息，请你写出一个结论；
(2)问前15位同学接水结束共需要几分钟?
(3)小敏说：“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟．”你说可能吗?请说明理由．
参考答案
1.D
2、（1）中位数是9119元
（2）2004、2005年某市城市居民人均可支配收入比上一年增加了1000元以上
（3）1872
3、D
4、（0，0），（0，
），（0，-3）
5、答案不唯一，符合要求即可
6、（1）
；
………………（2分）
（2）－x2＋２x
，１，
； （每格2分） ……………（６分）
（3）设AB长为m，那么AD为
S=·=－
． ……………（2分）
当＝
时，Ｓ最大． ……………（2分）
7、（1）直线AB解析式为：y=
x+． ……………（3分）
（2）方法一：设点Ｃ坐标为（x，x+），那么OD＝x，CD＝x+．
∴
＝
＝
． ………（2分）
由题意： ＝
，解得
（舍去） ………（2分）
∴ Ｃ（２，
） ………（１分）
方法二：∵ 
,＝，
∴
．…（2分）
由OA=OB，得∠BAO＝30°，AD=CD．
∴ 
＝
CD×AD＝
＝
．可得CD＝． ………（2分）
∴ AD=１，OD＝２．∴C（２，）． ………（1分）
（３）当∠OBP＝Rt∠时，如图
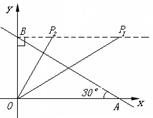①若△BOP∽△OBA，则∠BOP＝∠BAO=30°，BP=OB=3，
∴
（3，）． ……（2分）
②若△BPO∽△OBA，则∠BPO＝∠BAO=30°,OP=OB=1．
∴
（1，）． …………（１分）
当∠OPB＝Rt∠时
③ 过点P作OP⊥BC于点P(如图)，此时△PBO∽△OBA，∠BOP＝∠BAO＝30°
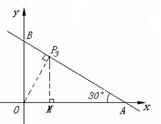过点P作PM⊥OA于点M．
方法一： 在Rt△PBO中，BP＝OB＝
，OP＝BP＝
．
∵ 在Rt△PＭO中，∠OPM＝30°，
∴ OM＝OP＝；PM＝OM＝
．∴
（，）． ……（1分）
方法二：设Ｐ（x ，x+），得OM＝x ，PM＝x+
由∠BOP＝∠BAO,得∠POM＝∠ABO．
∵tan∠POM==
=
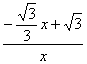，tan∠ABOC=
=．
∴x+＝x，解得x＝．此时，（，）． ……（1分）
④若△POB∽△OBA(如图)，则∠OBP=∠BAO＝30°，∠POM＝30°．
∴ PM＝OM＝
．
∴ 
（，）（由对称性也可得到点的坐标）．…………（2分）
当∠OPB＝Rt∠时，点P在ｘ轴上,不符合要求.
综合得，符合条件的点有四个，分别是：
（3，），（1，），（，），（，）．
8、B
9.略