中考数学最新题型精选（三）
1、如图1所示，一张三角形纸片ABC，∠ACB=
，AC=8，BC=6。沿斜边AB的中线CD把这张纸片剪成
两个三角形(如图2所示)。将纸片
沿直线
方向平移（点
始终在同一直线上），当点
与点B重合时，停止平移。在平移的过程中，
交于点E，
与
分别交于点F、P。
⑴当平移到如图3所示位置时，猜想
的数量关系，并证明你的猜想；
⑵设平移距离
为x，重复部分面积为y，请写出y与x的函数关系式，以及自变量的取值范围；
⑶对于⑵中的结论是否存在这样的x，使得重复部分面积等于原△ABC纸片面积的
？若存在，请求出x的值；若不存在，请说明理由。
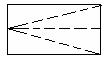
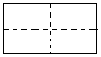2、现有一张长和宽之比为2：1的长方形纸片，将它折两次（第一次
折后也可打开铺平再者第二次），使得折痕将纸片分为面积相等
且不重叠的四个部分（称为一次操作），如图甲（虚线表示折痕）．
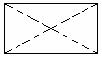
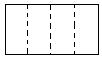除图甲外，请你再给出三种不同的操作，分别将折痕画在图①至
图③中（规定：一个操作得到的四个图形，和另一个操作得到的
四个图形，如果能够“配对”得到四组全等的图形，那么就认为是 （乙）
相同的操作，如图乙和图甲示相同的操作）．
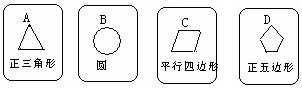
3、有四张背面相同的纸牌A，B，C，D，其正面分别划有四个不同的稽核图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
（1）用树状图（或列表法）表示两次模牌所有可能出现的结果（纸牌可用A、 B、C、D表示）；
（2）求摸出两张牌面图形都是中心对称图形的纸牌的概率．
 |
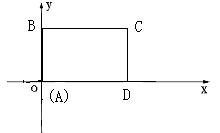
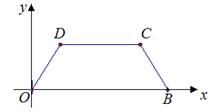
4、如图所示，在直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB＝3，AD＝5．若矩形以每秒2个单位长度沿x轴正方向作匀速运动．同时点P从A点出发以每秒1个单位长度沿A－B－C－D的路线作匀速运动．当P点运动到D点时停止运动，矩形ABCD也随之停止运动．
（1）求P点从A点运动到D点所需的时间；
（2）设P点运动时间为t（秒）。
①当t＝5时，求出点P的坐标；
②若⊿OAP的面积为s，试求出s与t之间的函数关系式（并写出相应的自变量t的取值范围）．
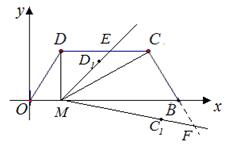
5、如图，在平面直角坐标系中，O为坐标原点为，B（5,0），M为等腰梯形OBCD底边OB上一点，OD＝BC＝2，∠DMC＝∠DOB＝60°．
(1)求直线CB的解析式；
(2)求点M的坐标；
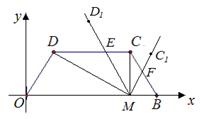
(3)∠DMC绕点M顺时针旋转α（30°＜α＜60°）后，得到∠D1MC1（点D1，C1依次与点D，C对应），射线MD1交直线DC于点E，射线MC1交直线CB于点F，设DE＝m，BF＝n .求m与 n的函数关系式．
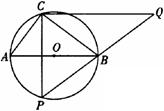
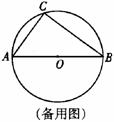
6、半径为2.5的⊙O中，直径AB的不同侧有定点C和动点P．已知BC ：CA＝4 : 3，点P在弧AB上运动，过点C作CP的垂线，与PB的延长线交于点O.
(l）当点P与点C关于AB对称时，求CQ的长；
(2）当点P运动到弧AB的中点时，求CQ的长；
(3）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长．
参考答案
1、（1）
.（1分）
因为
，所以
.
又因为
，CD是斜边上的中线，
所以，
，即
所以，
，所以
（2分）
所以，
.同理：
.
又因为
，所以
.所以（3分）
（2）因为在
中，
，所以由勾股定理，得
即
又因为
，所以
.所以
在
中，
到
的距离就是
的
边上的高，为
.
设
的
边上的高为
，由探究，得
，所以
.
所以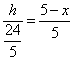
.
（5分）
又因为
，所以
.
又因为
，
.
所以
，
而
所以
（8分）
（1） 存在.当
时，即
整理，得
解得，
.
即当
或
时，重叠部分的面积等于原面积的.（10分）
2、距离如下：
 |  |  |
3、
第一次摸的牌
第二次摸的牌
（列表略）
（2）
4、（1）P点从A点运动到D点所需的时间＝（3+5+3）÷1＝11（秒）---- (3分)
（2）①当t＝5时，P点从A点运动到BC上，
此时OA=10,AB+BP=5，∴BP=2 (4分)
过点P作PE⊥AD于点E，则PE=AB=3,AE=BP=2 (5分)
∴OD=OA+AE=10+2=12---- (6分)
∴点P的坐标为（12，3）． (7分)
②分三种情况：
i．当0＜t≤3时，点P在AB上运动，此时OA=2t,AP=t
∴s=
×2t×t=t
(8分)
ii．当3＜t≤8时，点P在AB上运动，此时OA=2t
∴s=×2t×3=3t
(10分)
iii．当8＜t＜11时，点P在CD上运动，此时OA=2t,AB+BC+CP= t
∴DP=(AB+BC+CD)-( AB+BC+CP)=11- t
∴s=×2t×(11-
t)=-t+11t
(12分)
综上所述，s与t之间的函数关系式是：
当0＜t≤3时，s=t；
当3＜t≤8时，s=3t；
当8＜t＜11时，s=-t+11t (13分)
5、（1）BC解析式：y=
(2) 略证 △ODM∽△BMC,
设OM=x，2×2＝x（5－x），x＝1或4,M （1，0）或（4，0）
（3）当M （1，0）时，△DME∽△CMF，
CF＝2＋n，DE＝m，∴2＋n＝2m ，即m＝1＋
当M(4 ，0) 时 
∴m＝2（2－n），即m＝4－2n 
6、（本题满分12分）
解：( l）当点P与点C关于AB对称时，CP⊥AB，设垂足为D.
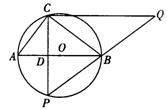∵AB为⊙O的直径，∴∠ACB=900.
∴AB=5,AC:CA=4:3,
∴BC=4, AC=3.
又∵AC·BC=AB·CD
∴ 
…………………………2分
在Rt△ACB和Rt△PCQ中，∠ACB＝∠PCQ=900, ∠CAB＝∠CPQ，
Rt△ACB∽Rt△PCQ
∴
……4分
(2）当点P运动到弧AB的中点时，过点B作BE⊥PC于点E（如图）.
∵P是弧AB的中点，
∴
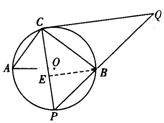…6分
又∠CPB=∠CAB
∴∠CPB= tan∠CAB=
∴
而从
……8分
由（l）得，
………………………………………9分
(3）点P在弧AB上运动时，恒有
故PC最大时，CQ取到最大值．………………………………………11分
当PC过圆心O，即PC取最大值5时，CQ 最大值为
……………12分