第五章中心对称图形（二）测试题
姓名___________________ 得分____________
一、选择题（下列各题所给答案中,只有一个答案是正确的.每小题3分,共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选择 |
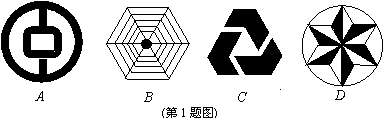1．(2006·连云港)下列图案中，不是中心对称图形的是( )
2．在半径为R的圆O中，所对弦中最长的圆周角是
A．60的圆周角 B．90
的圆周角 C．120的圆周角 D．150的圆周角
３．(2006·福州)已知AB为⊙O的弦,OC⊥AB,垂足为C,若OA= 10,AB=16, 则OC的长为 A.12 B.10 C.6 D.8
4.（ 2006·大连西岗）半径为4和2的两圆相外切，则其圆心距为
A.2 B.3 C.4 D.6
5.点P到⊙O上各点的最大距离为5，最小距离为1，则⊙O 的半径为
A．2 B．4 C．2或3 D．4或6
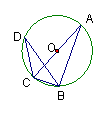
6.相交两圆的直径分别为2和8，则其圆心距d的取值范围是
A．d＞３ B．３＜d＜５ C．６＜d＜１０ D．３≤d≤５
７．（2006·安徽）下图是由10 把相同的折扇组成的“蝶恋花”（图 l ）和梅花图案（图 2 )（图中的折扇无重叠）, 则梅花图案中的五角星的五个锐角均为
A . 36º B . 42º C . 45º D . 48º
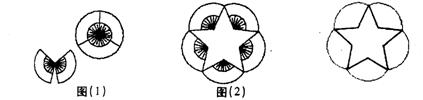
（第７题图）
８．（2006·淮安）一圆锥的侧面展开后是扇形，该扇形的圆心角为120°，半径为6cm，则此圆锥的表面积为
A．4
cm2 B．12cm2 C．16cm2 D．28cm2
９．(2006·宿迁)如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型．若圆的半径为r，扇形的半径为R，扇形的圆心角等于120°，则r与R之间的关系是 A．R＝2r B．R＝
r C．R＝3r D．R＝4
1０．边长为４的正方形的外接圆与内切圆组成的圆环的面积为
A．２
B．4
C．８ D．１６
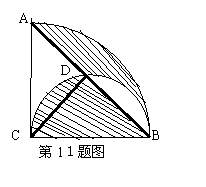
11．(2006·济宁).如图，以BC为直径，在半径为2圆心角为900的扇形内作半圆，交弦
AB于点D，连接CD，则阴影部分的面积是（ ）
A.
B. 
C. 
D. 
1２．(2006·武汉)如图，用半径R=3cm，r=2cm的钢球测量口小内大的内孔的直径D。测得钢球顶点与孔口平面的距离分别为a=4cm，b=2cm，则内孔直径D的大小为
A、9cm B、8cm C、7cm D、6cm
二、填空题（每题3分,共24分）
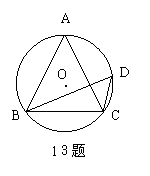
1３．（2006·大连）如图，⊙O中，∠ACB＝∠D＝60°，AC＝3，△ABC周长为______.
14．(2006·泰州)半径分别为6
和4的两圆内切，则它们的圆心距为 
.
15．(2006·厦门)两圆的半径分别为3cm和4cm，圆心距为2cm.,两圆的位置关系是____.
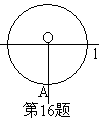1６． (2006·湖州)如图，⊙O的半径为4cm，
直线ι⊥OA，垂足为O，则直线ι沿射线OA向
平移________cm时与⊙O相切。
17．(2006·盐城)已知四边形ABCD内接于⊙O，
且∠A：∠C＝1∶2，则∠BOD＝_________. 第１８题
18．（2006·旅顺口）如图，点D在以AC为直
径的⊙O上，如果∠BDC＝20°，那么
∠ACB＝ ．
19. (2006·德州市)要在一个矩形纸片上画出半径分别是
和
的两个外切圆，该矩形面积的最小值是 __．
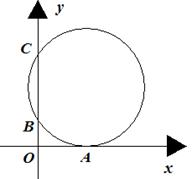
20．(2006·威海)如图，一圆与平面直角坐标系中的x
轴切于点A（8，0），与y轴交于点B（0，4），C（0，
16），则该圆的直径为 .
三、解答下列各题（21题8分，22、23每题9分，共26分） （第２０题图）
２1．(2006·广东) AB是OD的弦，半径OC、OD分别交AB于点E、F，且AE=BF，请你找出线段OE与OF的数量关系，并给予证明．
2２． (2006·江 西)如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交于D.
（1）请写出四个不同类型的正确结论；
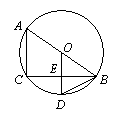（2）若BC = 8，ED = 2，求⊙O的半径.
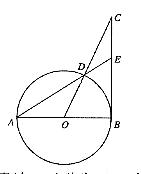2３．（2006·长春）如图，AB为⊙O直径，BC切⊙O于B，CO交⊙O交于D，AD的延长线交BC于E，若∠C
= 25°，求∠A的度数。
四、(本题满分9分)
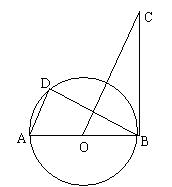
２４． (2006·三明梅列区)(本题满分10分)如图，AB是⊙O的直径，BC是⊙O的切线，D是 ⊙O上一点，且AD∥OC。（1）求证：△ADB∽△OBC；（2）若AB=2，BC=
，求AD的长。（结果保留根号）
五、(本题满分9分)
２５．某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．
（1）请你补全这个输水管道的圆形截面；
（2）若这个输水管道有水部分的水面宽AB＝16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．
六、(本题满分10分)
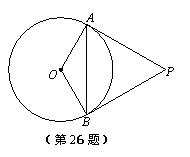
２６．(2006·宿迁)如图，PA、PB是⊙O的切线，A、B为切点，∠OAB＝30°．
（1）求∠APB的度数；（2）当OA＝3时，求AP的长．
七、(本题满分1２分) ．
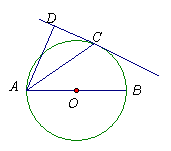
２７． (2006·南通)如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．（１）求证：AD⊥DC；（２）若AD＝2，AC＝，求AB的长．
八、(本题满分12分)
２６．
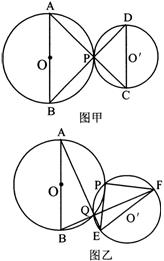(2006·盐城)已知：AB为⊙O的直径，P为AB弧的中点．（1）若⊙O′与⊙O外切于点P（见图甲），AP、BP的延长线分别交⊙O′于点C、D，连接CD，则△PCD是 三角形；
（2）若⊙O′与⊙O相交于点P、Q（见图乙），连接AQ、BQ并延长分别交⊙O′于点E、F，请选择下列两个问题中的一个作答：
问题一：判断△PEF的形状，并证明你的结论；
问题二：判断线段AE与BF的关系，并证明你的结论.
我选择问题 ，结论： .
证明：
九、(本题满分1２分)
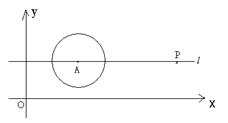
2９． (2006·泉州)如图，已知O为原点，点A的坐标为（4，3），
⊙A的半径为2．过A作直线
平行于
轴，点P在直线上运动．
（１）当点P在⊙O上时，请你直接写出它的坐标；
（２）设点P的横坐标为12，试判断直线OP与⊙A的位置关系，并说明理由.
（第２９题图）