九年级数学月考试题
(命题 校对 张正军)
(考试时间:120分钟,满分:150分)
第一部分 选择题(共36分)选择题答题表
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 11 | 12 |
| 答案 |
一、选择题(下列各题所给答案中,只有一个答案是正确的.每小题3分,共36分)
1.下列式子的结果是负数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列说法正确的是
A.近似数2.340有四个效数字 B.多项式a2b-3b+1是二次三项式
C.42°角的余角等于58° D.一元二次方程x2-5=0没有实数根
3.反比例函数![]() 的图象在每个象限内,
的图象在每个象限内,![]() 随
随![]() 的增大而减小,则
的增大而减小,则![]() 的值可为
的值可为
A.![]() B.0
C.1
D.2
B.0
C.1
D.2
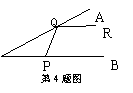 4.已知:如图,∠A0B的两边 0A、0B均为平面反光镜,∠A0B=
4.已知:如图,∠A0B的两边 0A、0B均为平面反光镜,∠A0B=![]() .
.
![]() 在0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是
在0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是
A.60° B.80°
 C.100 °
D.120°
C.100 °
D.120°
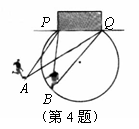
5.如图,在“世界杯”足球比赛中,甲带球向对方球门![]() 进攻.当他带球冲到
进攻.当他带球冲到![]() 点时,同伴乙已经助攻冲到
点时,同伴乙已经助攻冲到![]() 点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择 种射门方式.
点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择 种射门方式.
56.若关于![]() 的一元一次方程
的一元一次方程![]() 的解是
的解是![]() ,则
,则![]() 的值是
的值是
A. ![]() B.1
C.
B.1
C.![]() D.0
D.0
7.下列说法正确的是
A. 为了了解我市今年夏季冷饮市场冰淇淋的质量可采用普查的调查方式进行.
B. 为了了解一本300页的书稿的错别字的个数,应采用普查的调查方式进行.
C. 某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的平均数.
D.为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取1000份试卷进行统计分析,在这个问题中,样本是被抽取的1000名学生.
![]()
 8. 如图,在把易拉罐中水倒入一个圆水杯的过程中,若水杯中的水在点P与易拉罐刚好接触,则此时水杯中的水深为( )。
8. 如图,在把易拉罐中水倒入一个圆水杯的过程中,若水杯中的水在点P与易拉罐刚好接触,则此时水杯中的水深为( )。
A、2cm B、4cm C、6cm D、8cm
9.某超市(商场)失窃,大量的商品在夜间被罪犯用汽车运走.三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:
(1)罪犯不在甲、乙、丙三人之外;(2)丙作案时总得有甲作从犯;(3)乙不会开车.在此案中,能肯定的作案对象是( )
A.嫌疑犯乙 B.嫌疑犯丙 C.嫌疑犯甲 D.嫌疑犯甲和丙
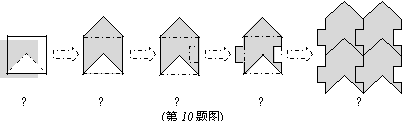
10.如图,把边长为2的正方形的局部进行图①~图④的变换,换成图⑤,则图⑤的面积是( )。
A、18 B、16 C、12 D、8
 |
![]() 11.下列图形中是轴对称图形的是( )。
11.下列图形中是轴对称图形的是( )。
 | |||||||
 |  | ||||||
 | |||||||
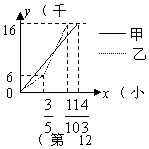
12.甲、乙两人骑车从学校出发,先上坡到距学校 6千米的![]() 地,再下坡到距学校16千米的
地,再下坡到距学校16千米的![]() 地,甲、乙两人行程
地,甲、乙两人行程![]() (千米)与时间
(千米)与时间![]() (小时)之间的函数关系如图所示.若甲、乙两人同时从
(小时)之间的函数关系如图所示.若甲、乙两人同时从![]() 地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论:①乙往返行程中的平均速度相同;②乙从学校出发45分钟后追上甲;③乙从
地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论:①乙往返行程中的平均速度相同;②乙从学校出发45分钟后追上甲;③乙从![]() 地返回到学校用时1小时18分钟;④甲、乙返回时在下坡路段相遇.其中正确的结论有( )
地返回到学校用时1小时18分钟;④甲、乙返回时在下坡路段相遇.其中正确的结论有( )
A.②③ B.①④ C.①②④ D.②③④
第二部分 非选择题(共114分)
| 得分 | 评卷人 |
请注意:考生必须将答案直接做在试卷上
二、填空题(每题3分,共24分)
13.计算:(![]() )(
)(![]() )=
.
)=
.
14.半径分别为6![]() 和4
和4![]() 的两圆内切,则它们的圆心距为
的两圆内切,则它们的圆心距为 ![]() .
.
15. 举世瞩目的长江三峡水利枢纽工程建成后,总装机容量为1820千瓦,年发电量为847亿千瓦时,将年发电量用科学记数法表示为______千瓦时.
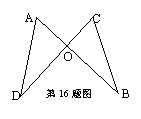
16.如图,AB、CD相交于点O,AB=CD,试添加一个条件使得△AOD≌△COB,你添加的条件是
(只需写一个).
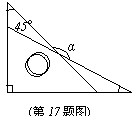
17.把一副三角板按如图方式放置,则两条斜边所形成的钝角α= 度。
 | |||
| | |||
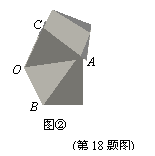
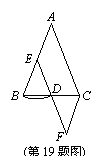
 18.将一张纸片沿任一方向翻折,得到折痕AB(如图①);再翻折一次,得到折痕OC(如图②);翻折使OA与OC重合,得到折痕OD(如图③);最后翻折使OB与OC重合,得到折痕OE(如图④)。展开恢复成图①形状,则∠DOE的大小是
度。
18.将一张纸片沿任一方向翻折,得到折痕AB(如图①);再翻折一次,得到折痕OC(如图②);翻折使OA与OC重合,得到折痕OD(如图③);最后翻折使OB与OC重合,得到折痕OE(如图④)。展开恢复成图①形状,则∠DOE的大小是
度。
 | |||
 | |||
19.在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连结ED并延长到点F,使DF=DE,连结FC,若∠B=70°,则∠F= 度。
![]() 20. 越来越多的商品房空置是目前比较突出的问题。据国家有关部门统计:2006年第一季度全国商品房空置面积达1.23亿平方米,比2005年第一季度增长23.8%。下列说法①2005年第一季度全国商品房空置面积为
20. 越来越多的商品房空置是目前比较突出的问题。据国家有关部门统计:2006年第一季度全国商品房空置面积达1.23亿平方米,比2005年第一季度增长23.8%。下列说法①2005年第一季度全国商品房空置面积为![]() 亿平方米;②2005年第一季度全国商品房空置面积为
亿平方米;②2005年第一季度全国商品房空置面积为![]() 亿平方米;③若按相同的增长率计算,2007年第一季度全国商品房空置面积达到1.23×(1+23.8%)亿平方米;④如果2007年第一季度全国商品房面积比2006年第一季度减少23.8%,那么2007年第一季度全国商品房空置面积与2005年第一季度相同。其中正确的是
亿平方米;③若按相同的增长率计算,2007年第一季度全国商品房空置面积达到1.23×(1+23.8%)亿平方米;④如果2007年第一季度全国商品房面积比2006年第一季度减少23.8%,那么2007年第一季度全国商品房空置面积与2005年第一季度相同。其中正确的是
A、①④ B、②④ C、②③ D、①③
| 得分 | 评卷人 |
三、解答下列各题(21题8分,22、23每题9分,共26分)
21.计算: ![]()
22.化简并求值: ![]() , 其中
, 其中![]()
23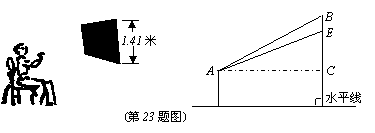 .如图,小刚面对黑板坐在椅子上。若把黑板看作矩形,其上的一个字看作点E,过点E的该矩形的高为BC,把小刚眼睛看作点A。现测得:BC=1.41米,视线AC恰与水平线平行,视线AB与AC的夹角为25°,视线AE与AC的夹角为20°,求AC和AE的长(精确到0.1米)。(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47。)
.如图,小刚面对黑板坐在椅子上。若把黑板看作矩形,其上的一个字看作点E,过点E的该矩形的高为BC,把小刚眼睛看作点A。现测得:BC=1.41米,视线AC恰与水平线平行,视线AB与AC的夹角为25°,视线AE与AC的夹角为20°,求AC和AE的长(精确到0.1米)。(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47。)
| 得分 | 评卷人 |
四、(本题满分9分)
24.如图,等腰![]() 中,
中,![]() ,
,![]() 是底边上的高,
是底边上的高,![]() .
.
(1)![]() 与
与![]() 有什么数量关系?请说明理由;
有什么数量关系?请说明理由;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ;
;![]() ,垂足为
,垂足为![]() ;
;![]() ,垂足为
,垂足为![]() ;
;![]() ,垂足为
,垂足为![]() ;…;
;…;![]() ,垂足为
,垂足为![]() ;
;![]() ,垂足为
,垂足为![]() (
(![]() 为非零自然数).若
为非零自然数).若![]() ,请用含
,请用含![]() 的代数式表示下表中线段的长度(请将结果直接填入表中);
的代数式表示下表中线段的长度(请将结果直接填入表中);
| 线段 |
|
|
| … |
|
| 长度 |
| … |
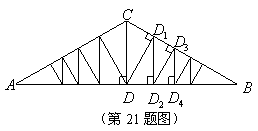 (3)某工业园区一个车间的人字形屋架为(2)中的图形,跨度
(3)某工业园区一个车间的人字形屋架为(2)中的图形,跨度![]() 为16米,
为16米,![]() 是该屋架的主柱,
是该屋架的主柱,![]() 为辅柱.若整个屋架有18根辅柱,则最短一根辅柱的长度约为多少米(结果精确到0.1米)?
为辅柱.若整个屋架有18根辅柱,则最短一根辅柱的长度约为多少米(结果精确到0.1米)?
| 得分 | 评卷人 |
五、(本题满分9分)
25.如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过点C的切线交ED的延长线于点P。
![]() (1)若PC=PF,求证:AB⊥ED;
(1)若PC=PF,求证:AB⊥ED;
(2)点D在劣弧AC的什么位置时,才能使AD2=DE·DF,为什么?
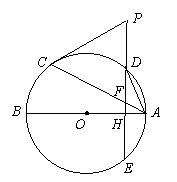
(第22题图)
| 得分 | 评卷人 |
六、(本题满分10分)
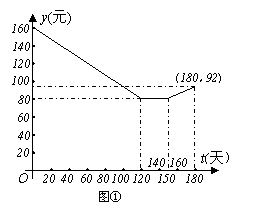
26.某茶厂种植“春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y(元)与上市时间t(天)的关系可以近似地用如图①中的一条折线表示。绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z(元)与上市时间t(天)的关系可以近似地用如图②的抛物线表示。
(1)直接写出图①中表示的市场销售电价y(元)与上市时间t(天)(t>0)的函数关系式;
(2)求出图②中表示的种植成本单价z(元)与上市时间t(天)(t>0)的函数关系式;
(3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?
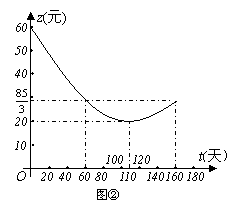 (说明:市场销售单价和种植成本单价的单位:元/500克。)
(说明:市场销售单价和种植成本单价的单位:元/500克。)
| 得分 | 评卷人 |
七、(本题满分10分)
27. 2006年6月5日(世界环境日),某市发布了一份空气质量抽样调查报告,其中该市1~5月随机调查得30天各空气质量级别的天数如下表:
| 空气污染指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 |
| 空气质量级别 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 |
| 天数 | 7 | 13 | 4 | 4 | 2 |
(1)请你估计该市2006年的空气质量主要是什么级别?
(2)请你根据抽样数据,预测该市2006年空气质量级别为优和良的天数共约有多少天?
(3)请你根据调查报告,对有关部门提几条建设“绿色城市”的建议。
| 得分 | 评卷人 |
八、(本题满分12分)
28.泰兴市政府为响应党中央建设社会主义新农村和节约型社会的号召,决定资助部分农村地区修建一批沼气池,使农民用到经济、环保的沼气能源。红星村共有360户村民,村里得到34万元的政府资助款,准备再从各户筹集一部分资金修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用的户数、修建用地情况见下表:
| 沼气池 | 修建费用(万元/个) | 可供使用户数(户/个) | 占地面积(m2/个) |
| A型 | 3 | 20 | 10 |
| B型 | 2 | 15 | 8 |
政府土地部门只批给该材沼气池修建用地188m2,若修建A型沼气池x个,修建两种沼气共需费用y万元。
(1)求y与x之间的函数关系式;
(2)试问有几种满足经上要求的修建方案?
(3)平均每户村民筹集500元钱,能否满足所需费用最少的修建方案。
| 得分 | 评卷人 |
九、(本题满分14分)
29. 如图,![]() 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,![]() 为原点,点
为原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() .
.
(1)在![]() 边上取一点
边上取一点![]() ,将纸片沿
,将纸片沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,求点
处,求点![]() ,
,![]() 的坐标;
的坐标;
(2)若过点![]() 的抛物线与
的抛物线与![]() 轴相交于点
轴相交于点![]() ,求抛物线的解析式和对称轴方程;
,求抛物线的解析式和对称轴方程;
(3)若(2)中的抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使
,使![]() 的内心在坐标轴上?若存在,求出点
的内心在坐标轴上?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 (4)(本小题为附加题,满分3分,计入卷面总分.如果你有时间,不妨试一试!)
(4)(本小题为附加题,满分3分,计入卷面总分.如果你有时间,不妨试一试!)
若(2)中的抛物线与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在线段
在线段![]() 上移动,作直线
上移动,作直线![]() ,当点
,当点![]() 移动到什么位置时,
移动到什么位置时,![]() 两点到直线
两点到直线![]() 的距离之和最大?请直接写出此时点
的距离之和最大?请直接写出此时点![]() 的坐标及直线
的坐标及直线![]() 的解析式.
的解析式.