九年级数学模拟试题(华师大版)
一、选择题(本题共10小题,每小题3分,共30分).
1.计算2-(-1)2等于( )
A.1 B.0 3.-1 D.3
2.化简x-y-(x+y)的最后结果是( )
A.0 B.2x C.-2y D.2x-2y
3．小明的妈妈为了奖励小明在学习中取得的进步，给小明新买了一个文具盆，你估计这个文具盒的厚度为3（ ）(填上合适的长度单位)。
A．mm; B．cm; C．dm; D．km
4. 方程x(x+3)=x+3的解是 ( )
A. x=1 B. x1=0, x2=－3
C. x1=1, x2=3 D. x1=1, x2=－3
5. 下列图中能过说明∠1>∠2的是 ( )
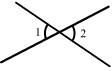
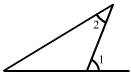
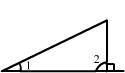
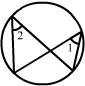
A. B. C. D.
6. 使一元二次方程
＝0有两个不相等的实数根的一个常数项是（ ）
A． 16； B． 64； C． 1； D． 20
7.某市社会调查队对城区内一个社区居民的家庭经济状况进行了调查,结果是:该社区共有500户,高收入、中等收入和低收入家庭分别有125户、280户和95户.已知该市有100万户家庭,下列表述正确的是( )
A.该市高收入家庭约25万户 B.该市中等收入家庭约56万户
C.该市低收入家庭约19万户
D.因为城市社区家庭经济状况良好,所以不能据此估计全市所有家庭经济状况
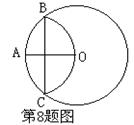
8.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC=( )
A.
B.
C.
D.
9. 方程组
的一个解是（
）
A
B 
C 
D 
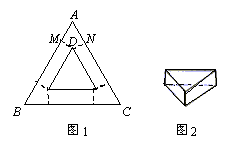10.用一块等边三角形的硬纸片（如图1）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图2），在△ABC的每个顶点处各剪掉一个四边形，其中四边形AMDN中，∠MDN的度数为（ ）
A. 100° B. 110°
C. 120° D. 130°
二、填空题(本题共5小题,每小题4分,共20分)
11. 两个不相等的实数m，n满足m2-6m=4，n2-6n=4，则mn的值为
12. 一根蜡烛在凸透镜下成一实像，物距u，像距v和凸透镜的焦距f满足关系式：＋＝. 若f＝6厘米，v＝8厘米，则物距u＝ 厘米.
13.已知平面直角坐标系上的三个点O（0，0）、A（－1，1）、B（－1，0），将△ABO绕点O按顺时针方向旋转135°,则点A、B的对应点A1、B1的坐标分别是A1（ ， ） ，B1( ， ) .
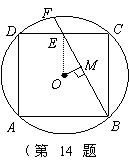
14. 如图,正方形ABCD内接于⊙O,E为DC的中点,
直线BE交⊙O于点F,如果⊙O的半径为
,则O点到BE
的距离OM=________.
15. 在平面直角坐标系中，横坐标、纵坐标都为整数的点
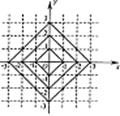称为整点．观察图中每一个正方形(实线)四条边上的整
点的个数，请你猜测由里向外第10个正方形(实线)四
条边上的整点个数共有_________个．
三、解答题
16. 计算:（1）
17. 解方程：
。
18. 先化简，再求值：
，其中
，
 |
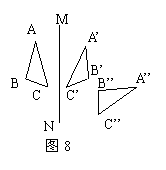19. 如图8，△ABC和△A’B’C’关于直线MN对称，
△A’B’C’和△A’’B’’C’’关于直线EF对称。
（1） 画出直线EF；
（2） 直线MN与EF相交于点O，∠BOB’’
与直线MN、EF所夹锐角α的数量关系是
20. 
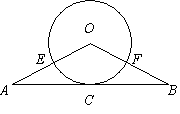如图，△ABO中，OA=OB，以O为圆心的圆经过AB的中点C，且分别交OA、OB于点E、F.
(1) 求证：AB是⊙O的切线；
(2) 若△ABO腰上的高等于底边的一半，且
，求
的长.
21.质检员为控制盒装饮料产品质量，需每天不定时的30次去检测生产线上的产品．若把从0时到24时的每十分钟作为一个时间段(共计144个时间段),请你设计一种随机抽取30个时间段的方法：使得任意一个时间段被抽取的机会均等,且同一时间段可以多次被抽取. (要求写出具体的操作步骤)
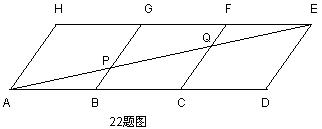
22、
如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，
（1） 若AB=6，求线段BP的长；（6分）
（2） 观察图形，是否有三角形与ΔACQ全等？并证明你的结论，（4分）
解：
23. 
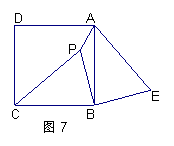已知：如图7，P是正方形ABCD
内一点，在正方形ABCD外有一点E，
满足∠ABE＝∠CBP，BE＝BP，
(1) 求证：△CPB≌△AEB；
(2) 求证：PB⊥BE；
(3) 若PA∶PB＝1∶2，∠APB＝135°,
求cos∠PAE的值.
24. 如图，已知直线L与◎○相切于点A，直径AB=6，点P在L上移动，连接OP交◎○于点C，连接BC并延长BC交直线L于点D，
（1）
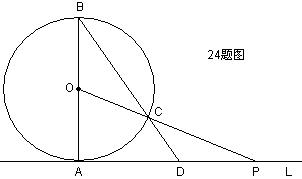若AP=4， 求线段PC的长（4分）
（2） 若ΔPAO与ΔBAD相似，求∠APO
的度数和四边形OADC的面积（答
案要求保留根号）（6分）
解：
25. 我国年人均用纸量约为28公斤，每个初中毕业生离校时大约有10公斤废纸；用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树，而平均每亩森林只有50至80棵这样的大树.
(1) 若我市2005年初中毕业生中环保意识较强的5万人,能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐.
(2) 宜昌市从2001年初开始实施天然林保护工程,到2003年初成效显著,森林面积大约由1374.094万亩增加到1500.545万亩.假设我市年用纸量的15％可以作为废纸回收、森林面积年均增长率保持不变，请你按宜昌市总人口约为415万计算:在从2005年初到2006年初这一年度内，我市新增加的森林面积与因回收废纸所能保护的森林面积之和最多可能达到多少亩.（精确到1亩）