九年级数学(上)期中考试卷(北师大版)
(总分:150分 时间:120 分钟)
姓名 考号 得分
一、 选择题(每小题4分,共40分)
1、等腰三角形一腰上的高与底边的夹角等于( )
A、顶角 B、顶角的一半 C、顶角的2倍 D、底角
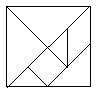 2、七巧板是我国古代的一项卓越创造,他虽然只有七块,但是可以拼出多种多样的图形。如图就是用七巧板拼成的一个正方形,则图中共有几对全等三角形(
)
2、七巧板是我国古代的一项卓越创造,他虽然只有七块,但是可以拼出多种多样的图形。如图就是用七巧板拼成的一个正方形,则图中共有几对全等三角形(
)
A、1 B、2 C、3 D、4
3、若方程![]() 有两个实数根,则m( )
有两个实数根,则m( )
A、m≥4![]() B、m≤4 C、m≤4 且m≠0
D、m≠0
B、m≤4 C、m≤4 且m≠0
D、m≠0
4、C、D两点在线段AB的中垂线上,且∠ACB=50º,∠ADB=80º,则∠CAD的度数为( )
A、15º B、115º C、15º或115º D、30º或150º5、
5、如图:是由一些相同的小正方体构成的几何体的三视图,这几何体小正方体的个数最多、最少分别为( )
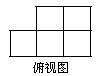
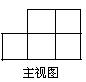
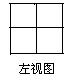
A、9个、7个 B、8个、7个
C、8个、6个 D、7个、6个
6、顺次连接四边形各边中点所得的四边形是矩形,则原四边形( )
A、对角线互相垂直 B、对角线相等
C、对角线互相垂直且相等 D、是正方形
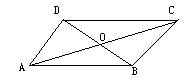 7、如图,
7、如图,![]() ABCD 中,对角线AC和BD相交与点O,如果AC=12,BD=10,AB=m,则m的取值范围是( )
ABCD 中,对角线AC和BD相交与点O,如果AC=12,BD=10,AB=m,则m的取值范围是( )
A、1﹤m﹤11 B、2﹤m﹤22
C、10﹤m﹤12 D、5﹤m﹤6
8、若点(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )都是反比例函数
)都是反比例函数![]() 的图象上的点,并且
的图象上的点,并且![]() ﹤0﹤
﹤0﹤![]() ﹤
﹤![]() ,则下列各式中正确的是( )
A、
,则下列各式中正确的是( )
A、![]() ﹤
﹤![]() ﹤
﹤![]() B、
B、![]() ﹤
﹤![]() ﹤
﹤![]()
C、![]() ﹤
﹤![]() ﹤
﹤![]() D、
D、![]() ﹤
﹤![]() ﹤
﹤![]()
9、图中是一个物体在不同时刻太阳光下的影子,按照时间的先后顺序,正确的是( )
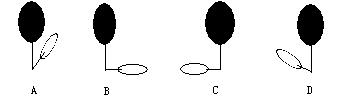
A、A→B→C→D B、D→B→C→A
C、C→D→A→B D、A→C→B→D
10、反比例函数![]() 与一次函数
与一次函数![]() 在同一坐标系中的图象大致是图中的(
)
在同一坐标系中的图象大致是图中的(
)
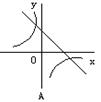
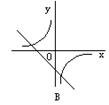
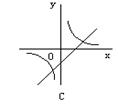
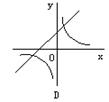
二、填空题(每小题3分,共30分)
1、已知![]() 是方程
是方程![]() 的一个根,则代数式
的一个根,则代数式![]() 的值等于 。
的值等于 。
2、下列命题:①等腰三角形的角平分线、中线和高线重和;②对角线互相垂直平分的四边形是菱形;③假命题没有逆命题;④晚上人在路灯下行走时,离路灯越远,影子就越长。其中真命题的序号是 。
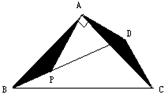
3、如图,△ABC中,∠BAC=90°,将△ABP绕点A逆时针旋转后,能将△ACD重合,如果AP=3,那么PD的长等于 。
 4、已知反比例函数
4、已知反比例函数![]() 的图象的两分支在第二、四象限,则
的图象的两分支在第二、四象限,则![]() 的值为
。
的值为
。
5、三角形两边的长为3和6,第三边是方程![]() 的解,则这个三角形的周长是 。
的解,则这个三角形的周长是 。
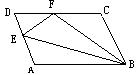 6、如图:ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的F点,若△FDE的周长为8,△FCB的周长为22,则FC的长为
。
6、如图:ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的F点,若△FDE的周长为8,△FCB的周长为22,则FC的长为
。
7、关于![]() 的一元
的一元![]() 的两根为
的两根为![]() =1,
=1,![]() =2,则
=2,则![]() 分解因式的结果为
。
分解因式的结果为
。
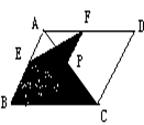 8、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB余E,PF∥CD交AD余F,则阴影部分的面积是
。
8、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB余E,PF∥CD交AD余F,则阴影部分的面积是
。
9、若a、b是方程![]() 的两根,则
的两根,则![]() 的值是 。
的值是 。
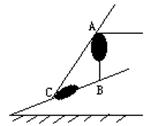 10、如图,一斜坡的倾斜角为30°,坡上有一树AB,当阳光与水平线成60°照射时,树影BC在斜坡上且长为6m,则树高为
m。
10、如图,一斜坡的倾斜角为30°,坡上有一树AB,当阳光与水平线成60°照射时,树影BC在斜坡上且长为6m,则树高为
m。
赵家中学九年级(上)期中考试答题卷
姓名 考号 得分
一、 选择题(每小题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、 填空题(每小题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
三、 解答题(每小题6分,共18分)
21、解方程:
(1)、(X-2)(X+3)=-6 ![]() (2)、
(2)、![]()
(3)、4![]() +4
+4![]() —3=0(用配方法)
—3=0(用配方法)
四、 解答题(每小题10分,共30分)
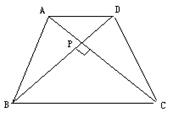
22、阅读材料,如图所示,在四边形ABCD中,对角线AC⊥BD,垂足为P,求证:![]() 。
。
证明:![]() →
→![]() →
→![]()
![]()
![]()
解答问题:
(1)上述证明得到的性质可叙述为
(2)已知如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于P点,AD=3cm,BC=7CM,利用上述性质求等腰梯形的面积。
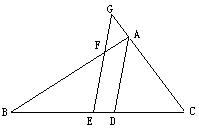 23、如图,AD是△ABC的角平分线,E是BC的中点,过E作EG∥AD交AB于F,交CA的延长线于G。
23、如图,AD是△ABC的角平分线,E是BC的中点,过E作EG∥AD交AB于F,交CA的延长线于G。
求证:BF=CG。
24、是否存在整数![]() ,使得关于
,使得关于![]() 的一元二次方程
的一元二次方程![]() 与
与![]() 的根都是整数?如果有,试求出
的根都是整数?如果有,试求出![]() 的值;如果没有,请说明理由。
的值;如果没有,请说明理由。
五、解答题(第25题10分,第26题12分,共22分)
25、某种新产品的进价是120元,在试销阶段发现每件产品的售价(元)与日销售量(件)始终存在下表中的数量关系:
| 每件售价(元) | 130 | 150 | 165 |
| 每日销售量(件) | 70 | 50 | 35 |
(1) 请你根据上表所给的数据表述出每件售价提高的数量(元)与日销售量减少数量(件)之间的关系。
(2) 在不改变上述关系的情况下,请你帮助商场经理策划每件商品定价为多少元时?每日盈利可达到1600元?
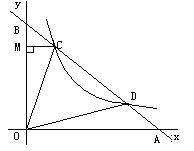 26、如图所示,已知C(
26、如图所示,已知C(![]() ,
,![]() )、D(
)、D(![]()
![]() )是双曲线
)是双曲线![]() 在第一象限内的分支上的两点,直线CD分别交
在第一象限内的分支上的两点,直线CD分别交![]() 轴、
轴、![]() 轴于A、B两点,连接OC、OD。
轴于A、B两点,连接OC、OD。
(1)、求证:![]() ﹤OC﹤
﹤OC﹤![]()
(2)、若∠BOC=∠AOD,CM⊥![]() 轴于M,且
轴于M,且![]() ,OC=
,OC=![]() ,求直线CD的关系式
,求直线CD的关系式