九年级数学第26章检测题
一、填空题(每题3分，共30分)
1、若二次函数
，当x取
(
)时，函数值相等，则当x取
时，函数值为 ．
2、抛物线和
的图像形状相同，对称轴平行于y轴，且顶点坐标为(－1，3)，则它的解析式为 ．
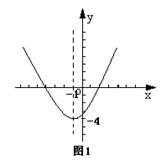
3、二次函数
的图像如图1所示，则函数值y<0时，对应x的取值范围是 ．
4、已知二次函数的图像开口方向下，且于y轴的正半轴相交，请你写出一个满足条件的二次函数解析式 ．
5、请你写出函数
与
具有的一个共同的性质 ．
6、某校运动会上，张强同学推铅球时，铅球行进的高度y(米)与水平距离x(米)之间的函数关系是
，张强同学的最好成绩是 米．
7、利用函数图像求得方程
的解是 ．
8、抛物线
与x轴的交点个数是
．
9、若二次函数
的图像与x轴有且只有一个交点，那么a的值和交点坐标分别是 ．
10、已知抛物线
经过点
和
，则
的值为 ．
二、选择题(每题4分，共32分)
11、已知抛物线
的顶点在x轴上，则b的值一定是（ ）
A．1 B． 2 C．－2 D．2或－2
12、把抛物线的图像向右平移3个单位，在向下平移2个单位，所得图像的解析式是
，则有（ ）
A．b=3，c=7 B．b=－9，c=－15
C．b=3，c=3 D．b=－9，c=21
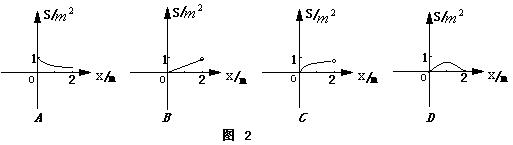
13、周长是4的矩形，它的面积S(m2)与一边长x(m)的函数图像大致是如图2中的（ ）
14、已知抛物线
，且
，则一定有（ ）
A．
>0 B．=0C． <0 D．≤0
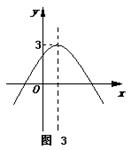
15、已知抛物线
如图3所示，则关于x的方程
的根的情况是（ ）
A．有两个不相等的正实数根 B．有两个异号实数根
C．有两个相等的实数根 D．没有实数根
16、当k取任意实数时，抛物线
的顶点所在的曲线是（ ）
A．
B．
C．
D．
17、已知关于x的方程
的一个根为
=2，且二次函数
的对称轴直线是x=2，则抛物线的顶点坐标是（ ）
A．(2，－3 ) B．(2，1) C．(2，3) D．(3，2)
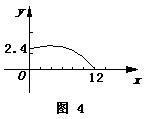18、为了备战世界杯，中国足球队在某次训练中，一队员在距离球门12m处的挑射正好射中了2．4m高的球门横梁，若足球运行的路线是抛物线(如图4所示)则下列结论:①
，②
，③
，④
其中正确的结论是（ ）
A．①③ B．①④ C．②③ D．②④
三、解答题(共38分)
19、已知抛物线
(1)确定此抛物线的顶点在第几象限；
(2)假设抛物线经过原点，求抛物线的顶点坐标．
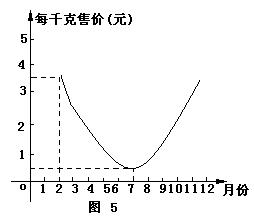20、某农场种植一种蔬菜，销售员张平根据往年的销售情况，对今年这种蔬菜的销售价格进行了预测，预测情况如图5所示，图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系．观察图像，你能得到关于这种蔬菜销售情况的哪些信息？
要求：(1)请提供四条信息；(2)不必求函数的解析式．
21、某工厂生产A产品x吨需费用P元，而卖出x吨这种产品的售价为每吨Q元，已知
．
(1)写出该厂生产并售出x吨这种产品所获利润W(元)关于x(吨)的函数关系式．
(2)当生产多少吨这种产品，并全部售出时，获利最多？这时获利多少元？这时每吨的价格又是多少远？
22、某化工材料经销公司购进了一种化工原料共7000千克，购进价格为每千克30元．物价部门规定其销售价格不得高于每千克70元，也不得低于30元，市场调查发现：单价定为70元时，日均销售60千克；单价每降低1元，日均多售出2千克．在销售过程中，每天还要支出其他费用500元(天数不足一天时，按一天计算)，设销售单价为x元，日均获利y元．
(1)求y关于x的二次函数关系时，并注明x的取值范围．
(2)将(1)中所求的二次函数关系式配方成
形式，写出顶点坐标，在坐标系中画出草图；观察图像指出单价定为多少元时日均获利最多，是多少？
参考答案
一、1、c 2、
3、－3<x<1 4、答案不惟一，只要满足二次项系数小于0且常数项大于0即可．如
5、答案不惟一，如：开口向上，与y轴交于(0，1)点等． 6、10 7、
8、两个 9、a=1，
(－1，0)；
a=9，(
，0) 10、
二、11、D 12、A 13、D 14、A 15、C 16、A 17、C 18、B
三、19、解：(1)
所以抛物线的顶点坐标为
，在第2象限．
(2)因为抛物线经过原点，所以
所以
所以顶点坐标为(－1，1)
20、解：(1)2月份每千克销售价格为3．5元
(2)1月到7月的销售价逐月下降
(3)7月到12月销售价逐月上升；
(4)2月与7月的销售差价为每千克3元；
还有其他合适的答案．请同学们探索．
21、解(1)W=Qx－P=
(2)当x=150时，利润最大，最大利润为2000元，这是每吨售价为40元．
22、解：(1)
(2)
，顶点是(65，1950)，单价定为65元时，日均获利最多是1950元．