九年级数学第一学期第三次月考试卷
（卷一）
本卷满分100分 命题人：
一、选择题（本大题12个小题，每小题3分，共36分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个答案是正确的。
1．下列各式中，是最简二次根式的是（ ）。
A.
B.
C. 
D. 
2．三角形两边的长分别是8和6，第三边的长是一元二次方程
的一个实数根，则该三角形的面积是 （ ）
A. 24
B. 24或
C. 48 D.
3.方程x²－x＋2＝0根的情况是（ ）
A. 只有一个实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 没有实数根
4．下列语句中不正确的有（ ）
①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦
③圆是轴对称图形，任何一条直径都是它的对称轴 ④长度相等的两条弧是等弧
A．3个 B.2个 C.1个 D.4个
5. 由一已知点P到圆上各点的最大距离为5，最小距离为1，则圆的半径为（ ）
A．2或3 B. 3 C. 4 D. 2 或4
6．二次函数y=x2-(12-k)x+12,当x>1时，y随着x的增大而增大，当x<1时，y随着x的增大而减小，则k的值应取（ ）
A．12 B. 11 C. 10 D. 9
7. 下列四个函数中，y的值随着x值的增大而减小的是（ ）
A.
B. 
C. 
D. 
8.如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于（ ）
A. 8 B. 14 C. 8或14 D. -8或-14
9.把二次函数
的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式是（ ）
A.
B.
C.
D.
10.直线ａ上有一点到圆心O的距离等于⊙O的半径，则直线ａ与⊙O的位置关系是（ ）
A.相离 B.相切 C.相切或相交 D.相交
11．有一个多边形的边长分别是4cm、5cm、6cm、4cm、5cm，和它相似的一个多边形最长边为8cm，那么这个多边形的周长是( )
A．12cm B．18cm C. 32cm D. 48cm
12．下列图形既是轴对称图形，又是中心对称图形的是（ ）
 |
A B C D
二、填空题（本大题12个小题，每小题2分，共24分）
13．若x、y都为实数，且
，则
=________。
14．在班里随意抽取一个同学，在5月生日的概率是 .
15．已知D、E为△ABC的边AB、AC上的两点，且AB=8，AC=6，AD=4，AE=3，则 
∶
= .
16．若
是二次函数，则m= 。
17．已知二次函数
，当x＝_________时，函数达到最小值。
18．如果抛物线y=-
x2+（m+2）x+
m的对称轴为直线x=
，
则m 的值为_________．
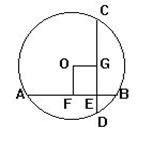
19．如图，⊙O中，弦AB⊥弦CD于E，OF⊥AB于F，OG⊥CD于G，
若AE=8cm，EB=4cm，则OG= cm。
20．若方程
的一个根为1，则另一个根为= .
21．相同时刻的物高与影长成比例，已知一电线杆在地面上的影长为30m，同时，高为1.2m的测竿在地面上的影长为2m，则可测得该电线杆的长是______m．
22．在Rt△ABC中，∠C=90°，AB=15cm，BC=10cm，以A为圆心，12cm为半径作圆，则点C与⊙A的位置关系是点C在⊙A ．
23．以坐标原点O为位似中心，作的位似图形，并把各边长放大到原来的5倍. 如果四边形ABCD的坐标A（2，3），B（4，0），C（6，0），D（5，5）那么它们的对应点的坐标 是 。（只要一种）
24.已知AB是⊙O的直径，AB=12cm,CD是⊙O一条弦，它与AB交于点E，⊿ACE与⊿BDE的面积之比为4:1,则AC：BD=_____
三、解答题（共40分）解答时请写出必要的演算过程或推理步骤。
25．（1）（4分）计算：
（2）（4分）解方程：
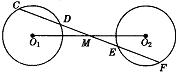
26.（6分）如图，已知⊙O1和⊙O2是等圆，直线CF顺次交这两个圆于C、D、E、F，且CF交O1O2于点M，
，O1M和O2M相等吗？为什么？
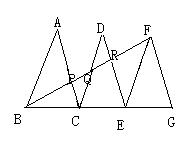
27.（6分）已知⊿ABC、⊿DCE、⊿FEG是三个全等的等腰三角形，底边BC、CE、EG 在同一直线上，且AB=
，BC=1。连接BF，分别交AC、DC、DE于点P、Q、R。求证：⊿BFG∽⊿FEG，并求BF的长。
28.（6分）已知一次函数y=－2x+c与二次函数y=ax2+bx－4的图象都经过点A(1，－1)，二次函数的对称轴直线是x=－1，请求出一次函数和二次函数的表达式.
29.（6分）将进货单价为70元的某商品按零售价100元/个售出时，每天能卖出20个，若这种商品的零售价在一定范围内每降价1元，其销售量就增加1个。如果你作为厂家的负责人：为了获得最大利润，则应降价多少元？此时最大利润是多少元？
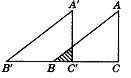
30．（8分）已知：在Rt△ABC中，∠C=90°，BC=4cm，AC=3cm．若△A′B′C′与△ABC完全重合，令△ABC固定不动，将△A′B′C′沿CB所在的直线向左以1cm/s的速度移动．设移动x秒后，△A′B′C′与△ABC的重叠部分的面积为ycm2．求：
（1）y与x之间的函数关系； （2）几秒钟后两个三角形重叠部分的面积等于
cm2？
