二次函数单元测试验 姓名
一、填空题
1.二次函数![]() 的对称轴方程是x=_______
的对称轴方程是x=_______
2.抛物线![]() 与x轴分别交于A、B两点,则AB的长为________.
与x轴分别交于A、B两点,则AB的长为________.
3.抛物线![]() 的顶点坐标是
。
的顶点坐标是
。
4.若将二次函数![]() 配方为
配方为![]() 的形式,则y=
.
的形式,则y=
.
5.函数![]() 的最小值是
的最小值是
 6.抛物线
6.抛物线![]() 可由抛物线
可由抛物线![]() 向 平移 个单位得到.
向 平移 个单位得到.
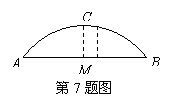
7.如图,一桥拱呈抛物线状,桥的最大高度是16米,跨度是40米,在线段AB上离中心M处5米的地方,桥的高度是 米.
8.当m=_____时,抛物线y=mx2+2(m+2)x+m+3的对称轴是y轴;当m=_____时,图象与y轴交点的纵坐标是1;当m=_____时,函数的最小值是-2.
二、选择题:
1.与抛物线![]() 的形状大小开口方向相同,只有位置不同的抛物线是( )
的形状大小开口方向相同,只有位置不同的抛物线是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.二次函数![]() 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( ) A.
的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( ) A.![]() =4
B.
=4
B. ![]() =3
C.
=3
C. ![]() =-5 D.
=-5 D. ![]() =-1。
=-1。
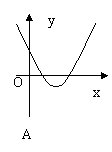
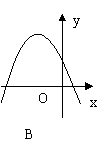
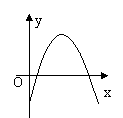
 3.如果
3.如果![]() ,那么二次函数
,那么二次函数![]() 的图象大致是( )
的图象大致是( )
 |  |  | |||
C
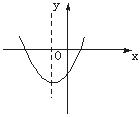 4.若二次函数y=ax2+bx+c的图象如右图,则点(a+b,ac)在( )
4.若二次函数y=ax2+bx+c的图象如右图,则点(a+b,ac)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.若二次函数y=x2-2x+c图象的顶点在x轴上,则c等于( )
A.-1
B.1
C.![]() D.2
D.2
6.小颖在二次函数y=2x2+4x+5的图象上,依横坐标找到三点(-1,y1),(![]() ,y2),
,y2),
(-3![]() ,y3),则你认为y1,y2,y3的大小关系应为( )
,y3),则你认为y1,y2,y3的大小关系应为( )
A.y1>y2>y3 B.y2>y3>y1 C.y3>y1>y2 D.y3>y2>y1
三、解答题:
1、已知二次函数y=(m2-2)x2-4mx+n的图象的对称轴是x=2,且最高点在直线y=![]() x+1上,求这个二次函数的表达式.
x+1上,求这个二次函数的表达式.
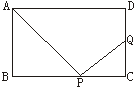
2.矩形ABCD的边AB=6 cm,BC=8 cm,在BC上取一点P,在CD边上取一点Q,使∠APQ成直角,设BP=x cm,CQ=y cm,试以x为自变量,写出y与x的函数关系式.并求出CQ的
最大值。
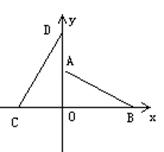 3.在直角坐标系中,⊿AOB的顶点坐标分别为A(0,2),O(0,0),B(4,0),把⊿AOB绕O点按逆时针方向旋转900到⊿COD。
3.在直角坐标系中,⊿AOB的顶点坐标分别为A(0,2),O(0,0),B(4,0),把⊿AOB绕O点按逆时针方向旋转900到⊿COD。
(1)求C,D两点的坐标;
(2)求经过C,D,B三点的抛物线解析式。
4.水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克. 经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
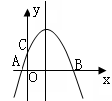 5.如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点。点A,C的坐标分别是(-1,0),(0,
5.如图,抛物线的对称轴是直线x=1,它与x轴交于A,B两点,与y轴交于C点。点A,C的坐标分别是(-1,0),(0,![]() )
)
(1)求此抛物线对应的函数解析式;
(2)若点P是抛物线上位于轴上方的一个动点,求△ABP的面积的最大值。
6、某瓜果基地市场部为指导某地某种蔬菜的生产和销售,在对历年市场行情和生产情况进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息.如图10(1)(2)两图.
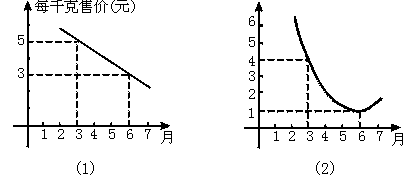
注:两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低;图10(1)的图象是线段,图10(2)的图象是抛物线段.
(1)在3月份出售这种蔬菜,每千克的收益是多少元?
(2)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
7.已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
并求出对称轴方程。
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
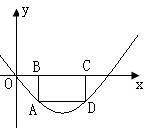 ①当BC=1时,求矩形ABCD的周长;
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由.