第一章 反比例函数
一、选择题
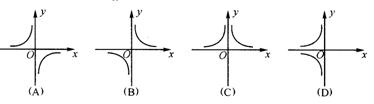
1.反比例函数
的图像大致是（ ）
2.如果函数y=kx-2（k≠0）的图像不经过第二象限，那么函数
的图象一定在( )
A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限
3. 如图，某个反比例函数的图像经过点P，则它的解析式为（ ）
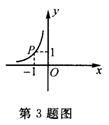A.
B.
C. 
D.
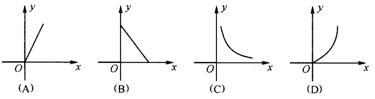
4. 某村的粮食总产量为a（a为常数）吨，设该村的人均粮食产量为y
吨，人口数为x，则y与x之间的函数关系式的大致图像应为（ ）
5. 如果两点
（x1，
）和
（x2，
）都在反比例函数y=
的图象上，如果x1<x2<0那么（ ）
A．＜＜0 B．
＜
＜0 C．＞＞0 D．＞＞0
6. 如果反比例函数y=
的图像经过点（2，3），那么次函数的图像经过点（ ）
A.(-2,3) B.(3,2) C.(3,-2) D.(-3,2)
二、填空题
7.已知点（1，—2）在反比例函数的图像上，则k= .
8.一个图像不经过第二、四象限的反比例函数的解析式为 .
9.已知反比例函数，补充一个条件：
后，使得在该函
数的图像所在象限内，y随x值的增大而减小.
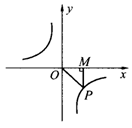
10、如图所示，△POM的面积为2，则该函数的解析式是_______________
11.近视眼镜的度数y与镜片焦距x（米）成反比例.已知400度近视眼镜镜片的焦
距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式是 .
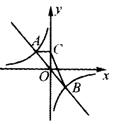
12.如图，函数y=—kx（k≠0）与y=—
的图像交于A、B两点．过点
A作AC垂直于y轴，垂足为C，则△BOC的面积为 .
三、解答题
13.一定质量的氧气，其密度ρ(kg/m,）是它的体积v (m,）的反比例函数．当V=10m3 时ρ＝1.43kg/m.
（1）求ρ与v的函数关系式；
（2）求当V=2m3时，氧气的密度．
14.已知圆柱的侧面积是6πm2，若圆柱的底面半径为x（cm)，高为ycm ).
（1）写出y关于x的函数解析式；
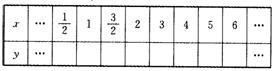
（2）完成下列表格：
（3）在所给的平面直角坐标系中画出y关于x的函数图像．
15.在某一电路中，保持电压不变，电流I（安培）与电阻R（欧姆）成反比例．当电阻R=5欧姆时，电流 I=2安培．
（l）求I与R之间的函数关系式；
(2)当电流I= 0.5 安培时，求电阻R的值；
(3)如果电路中用电器的可变电阻逐渐增大，那么电路中的电流将如何变化？
(4)如果电路中用电器限制电流不得超过10安培，那么用电器的可变电阻应控制在什么范围内？
16.某蓄水池的排水管每小时排水飞12m3, 8h可将满池水全部排空．
(1)蓄水池的容积是多少？
(2)如果增加排水管，使每小时的排水量达到x（m3)，那么将满池水排空所需的时间y（h）将如何变化？
(3)写出y与x之间的关系式；
(4)如果准备在6h内将满池水排空，那么每小时的排水量至少为多少？
(5)已知排水管每小时的最大排水量为24m3，那么最少多长时间可将满池水全部排空？
17. 反比例函数和一次函数y=mx+n的图象的一个交点A（-3，4），且一次函数的图像与x轴的交点到原点的距离为5.
(1)分别确定反比例函数与一次函数的解析式；
(2)设一次函数与反比例函数图像的另一个交点为B ，试判断∠AOB（点O为平面直角坐标系原点）是锐角、直角还是钝角？并简单说明理由．