函数测试卷
一、填空题：(每空1分,共65分)
1．函数
的取值范围是___________.
2．一次函数
的图象与x轴交点坐标是___________，与y轴交点坐标是___________图象与坐标轴所围成的三角形面积是___________.
3．点P（-3，2）关于
轴、原点对称的点的坐标分别为___________、___________.
4．若点A（-5，y1）、B（-2，y2）都在直线
上，则
____
（填“>”或“<”）.
5.二次函数y=2x2- 4x+ 3 通过配方化为顶点式为y= _________, 其对称轴是______,顶点坐标为_______,抛物线开口________,当x_______时,y随x 的增大而增大;当x____时,y随x的增大而减小;当x=______时,y最值=________.
6.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线的解析式为__________.
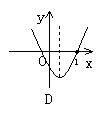7.已知抛物线y=ax2+bx+c(a≠0)的顶点为P(-2,3),且过A(-3,0), 则抛物线的关系式为________ ___.
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示, 则a、c 、 △( △= b2- 4ac)
与零的大小关系是a_____0,c____0,△_____0,(填入“>”、“<”或“=”)
9、已知点Ｐ在第三象限，且到ｘ轴的距离是３，到ｙ轴的距离是１，
则点Ｐ的坐标是
10. 已知点A的坐标是（a,b）.（1）当a＜0，b＞0时，点A位于 象限
（2）当a＜0,b=0时，点A位于 ；（3）当a为任意实数，b＞0时，点A位于 .
11.函数y=kx+3的图象过点(1，2)，则这个函数的解析式是_______.
12.如果直线y=(k-1)x+b-2不经过第一象限，则k的范围是_________, b的范围______ ___.
13．点P（-6，4）到x轴的距离为 ，到y轴的距离为 。
14.填表
| 函数解析式 | 开口方向 | 对称轴 | 顶点 坐标 | 最大（小）值 | 与x轴有无交点 | 与y轴交点 |
| y=2(x+3)2- 4 |
|
|
|
|
|
|
| y=x2-x+1 |
|
|
|
|
|
|
| y= -2x2 - 2 |
|
|
|
|
|
|
| y=2(x-2)(x+3) |
|
|
|
|
|
|
| h=1005t2 |
|
|
|
|
|
|
| y=x (8 - x) |
|
|
|
|
|
|
二、选择题：(每题2分,共22分)
1．若点P（n，n-1）在第四象限，则下列关系正确的是（ ）
A．0<n<1 B．n<0 C．n>0 D．n>1
2．已知直线
经过一、二、三象限，则有（ ）
A．k<0，b <0 B．k<0，b>0 C．k>0，b>0 D．k>0，b<0
3．一次函数
的图象不经过的象限是（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．若一次函数
的函数值
随的增大而增大，且此函数的图象不
经过第二象限，则
的取值范围是（ ）
A．
B．
C．
D．
或
5．点P在第二象限，点p到轴的距离为
、到轴的距离为1，则点P的坐标是（ ）
A．（-，1） B．（，-1） C．（-1，） D．（1，-）
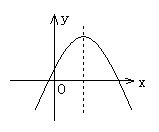
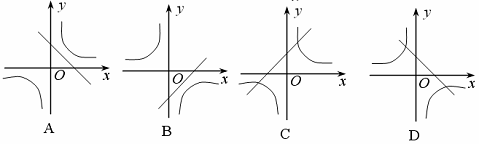
6．在同一直角坐标系中，函数
与
（k≠0）的图象大致是（ ）
7.若函数
是二次函数,那么m的值是( )
A.2
B.-1或3
C.3
D.
8.抛物线y=x2+3x的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有( )
A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a、b、c都小于0
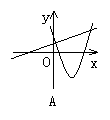
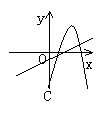
10.如图所示, 当b<0时, 函数y=ax+b与y=ax2+bx+c在同一坐标系内的图象可能是( )
 |  |  |  | ||||
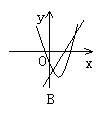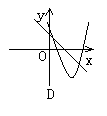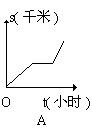
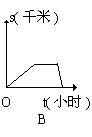
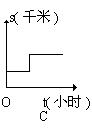
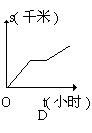
11.小明骑自行车上学，从家里出发后以某一速度匀速前进，中途由于自行车出了故障，
停下修车耽误了一段时间。为了按时到校，小明加快速度 (仍保持匀速)前进，结果准时
到达学校。下列能大致表示小明行进路程s(千米)与行进时间t(小时)之间关系的图象为( A )
三.解答题(33分)
1.(6分)小明在暑期社会实践活动中，以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售，在销售了40千克西瓜之后，余下的每千克降价0.4元，全部售完。销售金额与售出西瓜的千克数之间的关系如图所示。
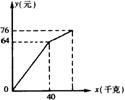请你根据图像提供的信息完成以下问题：
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式。
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
2．(9分)已知一次函数
的图象经过（2，-3）和（-4，-6）两点．
（1）求这个函数解析式并画出它的图象．
（2）根据图象回答：为何值时，
；为何值时，
．
（3）求此函数图象与两坐标轴所围成的三角形的面积．
3.已知y=y1+y2，且y1与x2成正比例，y2与x-1成反比例,当x=-1时，y=3；当x=2时，y=-3.(6分)
（1）求y与x之间的函数关系式；（2）求当x=
时,y的值.
4.(6分)根据下列条件,分别求出对应的二次函数关系式.
(1)已知抛物线的顶点是(-1,-2),且过点(1,10);
(2)已知抛物线过三点:(0,-2),(1,0),(2,3).
5.(6分)有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中.
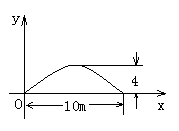(1)求这条抛物线所对应的函数关系式;
(2)在对称轴右边1m处,桥洞离水面的高是多少?