九年级（上）第四次月考数学试卷
班级 姓名 座号 得分
| 题号 | 一 | 二 | 三 | 四 | 五 | |||
| 20 | 21 | 22 | 23 | 24 | ||||
| 分数 | ||||||||
一、选择题（6×3′＝18′）
1．下列各式成立的是（ ）
A．
B.
C．
Ｄ．
2．下列说法正确的是（ ）
Ａ．圆的对称轴是圆的直径 Ｂ．相等的圆周角所对的弧相等
Ｃ．平分弦的直径垂直于弦，并且平分弦所对的两条弧
Ｄ．经过半径的外端并且垂直于这条半径的直线是圆的切线
3．用配方法解一元二次方程
，配方后得到的方程是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
４．用反证法证明“若a⊥c,b⊥c,则a∥b”，第一步应假设（ ）
Ａ． a∥b Ｂ．a与b垂直 Ｃ．a与b不一定平行 Ｄ．a与b相交
5．如图，下列各图中，绕点O旋转180°后能与原来位置重合的是（ ）
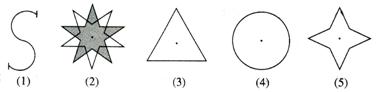
A．(1)(2)(4) B．（1）（2）（5） C．（1）（4）（5） D．（2）（3）（4）
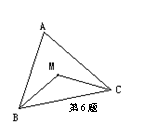
6．Ｍ是△ABC的内心，∠BMC=130°，则∠A的度数为（ ）
Ａ．60° Ｂ．65° Ｃ．70° Ｄ．80°
二．填空题（8×3′＝24′）
7．反比例函数
的图象与坐标轴有 个交点,图象在
象限,当
＞0时函数值
随的增大而
；
8．某果园有果树200棵，从中随机抽取5棵，每棵果树的产量如下（单位：千克）
98 102 97 103 105，这组数数据的中位数是 ，这5棵果树的平均产量为 千克，估计这200棵果树的总产量约为 千克；
9．代数式
在实数范围内有意义，则
的取值范围是 。
10．点P(
)与点Q
关于原点对称，则
。
11．⊙O的半径长为5cm，圆心到弦MN的距离OA＝3cm，则弦MN的长是 。
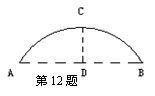
12．有一圆弧形的拱桥，拱的跨度AB=16米，拱高CD=4米，则桥拱的半径是 。
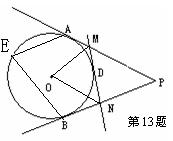13．如图，直线PA、PB、MN分别与⊙O相切于点A、B、D，
若PA=PB＝8cm，∠P=500，则△PMN的周长是 ，∠E= 。
∠MON=
三、计算题（5×5′＝25′）
15．
16．解方程：
17．解方程：
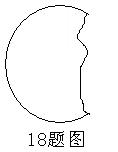
18．作图题：如图为残破的轮片，试找出轮片的圆心（写出作法，保留作图痕迹，不证明。）
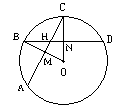
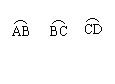19．已知，⊙O中， ＝ ＝ ，求证：∠B=∠C.
 |
四．解答题（3×10′＝30′）
20．振华校办工厂生产某种产品，今年产量为200件，计划通过改革技术，使今后两年的产量都比前一年增长相同的百分数，这样三年（包括今年）的产量达到1400件，求这个百分数。
21．已知方程
有两个相等的实数根，求
的值及方程的根。
五．综合题（2×9.5′＝19′）
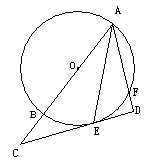
22． 已知：AB是⊙O的直径，AE平分∠BAF，交⊙O于点E，过点E作直线与AF垂直且交AF延长线于D，交AB延长线于C。求证：CD是⊙O的切线。
 |
23．已知△ABD和△ACE都是等边三角形，CD，BE相交于点F。
（1）求证：△ABE≌△ADC。．
（2）图中哪两个三角形可以通过怎样的旋转而相互得到？
（3）求∠BFC的度数。
 |
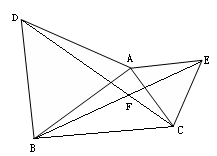已知二次函数ｙ＝ｘ2－（ｍ2+8）ｘ+2（ｍ2+6）
（1） 求证：不论取任何实数ｍ，此函数图像与轴都有两个交点，且两个交点都在ｘ轴的正半轴上
（2） 假设这个函数的图像与ｘ轴交于B、C两点，与ｙ轴交于A点，若△ＡＢＣ面积为48，求ｍ的值
（3） 投抛物线的顶点为P，是否存在实数ｍ，使△ＰＢＣ为等腰直角三角形，若存在，求出ｍ的值，若不存在，说明理由