《直角三角形的边角关系》知识要点及巩固练习
一、知识要点
1、三角函数定义：sinA= cosA= tanA= cotA=
2、特殊角的三角函数值：30°：sin30°= ， cos30°= ，tan30°= ，cot30°=
45°：sin45°= ， cos45°= ，tan45°= ，cot45°=
60°：sin60°= ， cos60°= ，tan60°= ，cot60°=
3、三角函数公式： ① sin(90°－A)=cosA； cos(90°－A)=sinA； tan(90°－A)=cotA； cot(90°－A)=tanA
② 
；
；
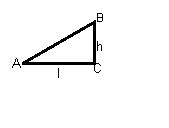4、在直角三角形中，除直角外，一共有5个因素，即3条边和2个锐角，由直角三角形中除直角外的已知元素（两边或者一边一锐角），求出所有未知元素的过程，叫做解直角三角形
5. 坡度与坡角的定义：
二、巩固练习
1、在Rt△ABC中，∠C=90°，a＝1，c＝4,则sinA的值是___。2、已知∠A+∠B=90°,且cosA=1/5，则cosB的值为____。3、已知α为锐角，tan（90°－α）=
，则α的度数为___。
4、在△ABC中，∠C=90°，BC=5，AB=13，则sinA的值是 _ _。
5、等腰三角形底边长为10㎝，周长为36cm，那么底角的余弦等于______
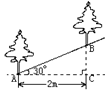
6、如右图，沿倾斜角为30°的山坡植树，要求相邻两棵树的水平距离AC为
2m，那么相邻两棵树的斜坡距离AB为 m。(精确到0.1m)
7、菱形ABCD的对角线AC=10，BD=6，则 tanA/2= _____
8、离旗杆20米处的地方用测角仪测得旗杆顶的仰角为
， 如果测角仪高为1.5米．那么旗杆的高是_________米（用含的三角函数表示）．
9、校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米。一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞__________米。
10、
|
|
|
11、下图为住宅区内的两幢楼，它们的高
，现需了解
|
甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求：
1）若两楼间的距离
时，甲楼的影子，落在乙楼上有多高？
|
|
2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？
 |
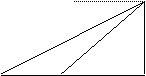12. 如图，从山顶A望地面C、D两点，它们的俯角分别为
、
，
若测得CD = 100米，求AB的高度；
