初三第二次月考——数学试卷
卷 一
一、选择题:(本题有12小题，每小题4分，共48分。每小题只有一个选项是正确的，不选、错选、多选均不给分)
1、计算：（＋2）＋（－1）的结果是（ ）
A、－1 B、1 C、2 D、3
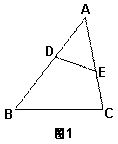
2、已知：如图1，在△ABC中，∠ADE＝∠C，则下列等式成立的是（ ）
A、 ＝ B、 ＝
C、 ＝ D、 ＝
3、下列图形中，不可能围成正方体的有（ ）个
A、1 B、2 C、3 D、4
4、计算
的结果是（ ）
A、 
B、 
C、
D、
5、下列图案中既是中心对称图形，又是轴对称图形的是( )
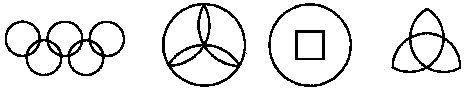A．
B．
C．
D．
6、抛物线
的对称轴是（ ）
A、x＝－2 B、x＝4 C、x＝2 D、x＝－4
7、有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼板3块，分别写有“20”, “08”和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”,则他们就给婴儿奖励。假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是（ ）
A、
B、
C、
D、
8、扇形的半径为30cm，圆心角为120０，用它做成一个圆锥的侧面，则圆锥底面半径为（ ）
Ａ、10 cm Ｂ、20 cm Ｃ、10π cm Ｄ、20π cm
9、钟老师出示了小黑板上的题目（如图）后，小敏回答：“方程有一根为1”，小聪回答：“方程有一根为2”。则你认为（ ）
A、只有小敏回答正确 B、只有小聪回答正确
C、小敏、小聪回答都不正确 D、小敏、小聪回答都正确
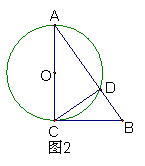
10、如图2，Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，以AC为直径的圆交AB于D，则AD的长为( )
A、 
B、 
C、
D、 4
11、现规定一种新的运算“
”：
，如
，则
＝（ ）
A、
B、8 C、 D、
12、一件衣服标价132元，若以9折降价出售，仍可获利10%，则这件衣服的进价是（ ）
A、106元 B、108元 C、118元 D、105元
卷 二
二、填空题:(本题有6小题，每小题5分，共30分)
13、在函数
中，自变量x的取值范围是___________________。
14、在实数范围内分解因式：a4－4＝ ________ 。
15、如果反比例函数的图象经过点（1，－2），那么这个反比例函数的解析式为_________________。
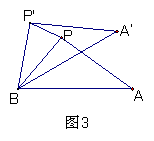16、如图3，如果△APB绕点B按逆时针方向旋转30°后得到△A′P＇B，且BP＝2，那么PP＇的长为________________。(不取近似值. 以下数据供解题使用：sin15°＝
，cos15°＝
)
17、某花圃用花盆培育某种花苗，经过试验发现每盆的盈利与每盆的株数构成一定的关系。每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆每增加1株，平均单株盈利就减少0.5元，要使每盆的盈利达到10元，每盆应该植 株。
18、已知一列数：1，―2，3，―4，5，―6，7，… 将这列数排成下列形式：
第1行 1
第2行 －2 3
第3行 －4 5 －6
第4行 7 －8 9 －10
第5行 11 －12 13 －14 15
… …
按照上述规律排下去，那么第50行从左边数第5个数等于 。
三、解答题:(本题有7小题，共72分)
19、（本题8分）计算：
20、（本题8分）如图，已知□ABCD中，E为AD的中点，CE的延长线交BA的延长线于点F。
⑴求证：CD＝FA；
⑵若使∠F＝∠BCF，□ABCD的边长之间还需再添加一个什么条件？
请你补上这个条件，并进行证明(不要再增添辅助线)。
21、(本题8分) 如图，已知在△ABC中，AB＝AC＝６，cosＢ ＝
点Ｏ在边AB上，
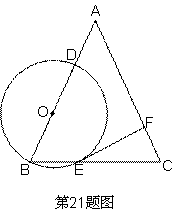⊙Ｏ过点B且分别与边AB、BC交于点D、E，且EF⊥AC，
垂足为F，设OB＝ｘ，CF＝ｙ。
（１）求证：直线EF是⊙Ｏ的切线；
（２）求ｙ关于ｘ的函数关系式（不要求写自变量的取值范围）。
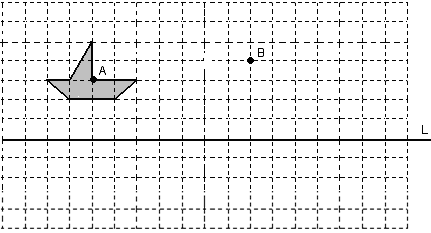
22、(本题10分)如图，有一条小船，
（1）若把小船平移，使点A平移到点B，请你在图中画出平移后的小船；
（2）若该小船先从点A航行到达岸边L的点P处补给后，再航行到点B，但要求航程最短，
试在图中画出点P的位置。
 |
23、(本题12分) 某县教育局在中学开展的“创新素质实践行”中，进行了小论文的评比。各校交论文的时间为5月1日至30日，评委会把各校交的论文的件数按5天一组分组统计，绘制了频率分布直方图，已知从左至右各长方形的高的比为2：3：4：6：4：1，第二组的频数为18。请回答下列问题：
（1）本次活动共有多少篇论文参加评比？
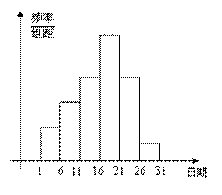（2）哪组上交的论文数量最多？有多少篇？
（3）经过评比，第四组和第六组分别有20篇、
4篇论文获奖，问这两组哪组获奖率较高？
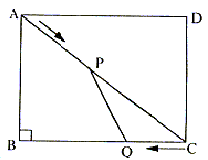
24、(本题12分) 如图，在矩形ABCD中，AB＝6米，BC＝8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从点C出发，沿CB向点B移动，设P、Q两点移动t秒（0＜t＜5）后，四边形ABQP的面积为S米2。
（1）求面积S与时间t的关系式；
（2）在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？
若能，求出此时点P的位置；若不能，请说明理由。
25、(本题14分) 已知抛物线
与y轴的交于C点，C点关于抛物线对称轴的对称点为C′。
（1）求抛物线的对称轴及C、C′的坐标（可用含m的代数式表示）；
（2）如果点Q在抛物线的对称轴上，点P在抛物线上，以点C、C′、P、Q为顶点的四边形是平行四边形，求Q点和P的坐标（可用含m的代数式表示）；
（3）在（2）的条件下，求出平行四边形的周长。