初三第一次月考数学试题
(考试时间：120分钟，满分：150分)
一、选择题（下列各题所给答案中,只有一个答案是正确的.每小题4分,共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1．在有理式
，
，
，
，
，
，
中分式的个数
A．2个 B．3个
C．4个 D．5个
2．下列分式中，最简分式是：
A、
B、
C、
D、
3．如果关于x的方程(m-3)x
+mx+1=0是一元二次方程,则m为
A．－1 B．－1或3 C．3 D．1或-3
4．方程
的根的情况是
A．有两个不等的有理数根 B．有两个相等的有理数根
C．有两个不等的无理数根 D．有两个相等的无理数根
5．将（
）-1，（-2）0，（-3）2这三个数按从小到大的顺序排列，正确的结果是（ ）．
A．（-2）0<（）-1<（-3）2 B．（）-1<（-2）0<（-3）2
C．（-3）2<（-2）0<（）-1 D．（-2）0<（-3）2<（）-1
6．当 k等于（ ）时，
是互为相反数
A． B. C. D.
7．关于x的方程
有实数根，则k的取值范围是 （ ）
A、k<1 B、
C、k<1且k≠0 D、且k≠0
8．若分式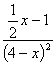
的值为正数，则x的值为（ ）．
A．x<2 B．2<x<4 C．x>2 D．x>2且x≠4
9．实数a，b满足ab=1，记M=
+
，N=
+
，则M、N的大小关系为（ ）．
A．M>N B．M=N C．M<N D．不确定
10．“五一”期间，几名同学包租一辆面包车前去A地游览，面包车的租价为180元，出发时，又增加了两名同学，结果每个同学比原来少分摊3元车费．若设参加旅游的学生共有x人，则所列方程为( )
(A) 
(B) 
(C) 
(D) 
二．填空题（每题4分,共20分）
11．生物学家发现一种病毒的长度约为0.000043毫米，用科学记数法表示为＿＿＿＿米．
12．有一个分式，三位同学分别说出了它的一些特点，甲：分式的值不可能为0；乙：分式有意义时x的取值范围是x≠±1；丙：当x=-2时，分式的值为1，请你写出满足上述全部特点的一个分式___________．
13．方程
的两个根，一个是－1，另一个是1，则
＝
，
＝ 。
14．如果
则 A=________ B＝________.
15．如果记y=
=f（x），并且f（1）表示当x=1时y的值，即f（1）=
=
；f（）表示当x=时y的值，即f（）=
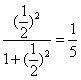，那么f（1）+f（2）+f（）+f（3）+f（
）+……+f（n）+f（
）=_______（结果用含n的代数式表示，n为正整数）．
三．解答下列各题
16．计算：（每题5分,共10分）
(1) 
（2） 
(sin45°－
)0－
17．按要求解方程（每题4分,共16分）
(1) （2x－1）2=81（直接开方法） (2) x2＋4x-1=0（配方法）
(3)x2-3x-4=0（因式分解法） (4)（x-2）（x-3）＝1(求根公式法)
18．解分式方程: （每题5分,共10分）
（1）
+1=
；
（2）
19． 已知： 
（6分）
20．已知三角形的三边长均满足方程
，试求这个三角形的面积。（10分）
21．“真棒”超市用50000元从外地采购一批“T恤衫”，由于销路好，又紧急调拨18．6万元采购比上次多2倍的“ T恤衫”，但第二次比第一次进价每件贵12元，超市在出售时统一按每件80元的标价出售，为了缩短库存时间，最后的400件按6．5折处理并很快售完，求超市在这笔生意上盈利多少元？（8分）
22．江滨房地产商向银行贷款800万资金用于房产开发，约定两年到期时一次性还本付息，利息是本金的11％，该地产商利用这笔贷款经营，两年到期时除还清贷款的本金和利息外，还盈余80万若在经营期间每年比上一年资金增长的百分数相同，求这个百分数。（8分）
23．（阅读理解题）阅读下面的解题过程，然后解题：
题目：已知
求x+y+z的值
解：设=k,
则x=k(a-b)，y=k(b-c), z=k(c-a),
于是，x+y+z=k(a-b+b-c+c-a)=k·0=0
仿照上述方法解答下列两题：
（1）
，且a+b+c≠0，求k的值。（5分）
（2）已知：
（5分）
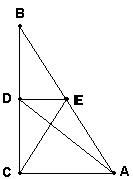
24．在直角三角形ABC中，∠ACB=900，AB=10，BC=8。点D在BC上运动（不运动到B、C），DE∥CA，交AB于E．设BD＝ｘ，△ADE的面积为y．
（1）求y与X的函数关系式,及自变量ｘ的取值范围；（5分）
（２）用配方法说明何时△ADE的面积最大，最大面积是多少？（4分）
（３）求当tan∠ECA＝４时，△ADE的面积。 （3分）
