初三数学教学质量摸底试卷
一. 选择题(每小题3分,共30分)
1. ![]() 的绝对值是( )
的绝对值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2. 当![]() 时,代数式
时,代数式![]() 的值是( )
的值是( )
A. 2 B. 0 C. 4 D. 1
3. 要使分式![]() 有意义,则的取值范围是( )
有意义,则的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 抛物线![]() 与
与![]() 轴的交点坐标是( )
轴的交点坐标是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
5. 如图所示,已知DE//BC,AD = 3, BD = 6,EC = 4,则AE长为( )
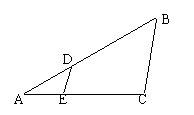
A. 2 B. 4 C. 1 D. 3
6. 用地砖铺地面,下列哪种正多边形地砖不能铺满地面
A.  B.
B. 
C. D.
D. 
7. 已知抛物线![]() 的图象与x轴有两个交点,则
的图象与x轴有两个交点,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8. 某商店举办有奖销售活动,办法如下:凡购满100元者得奖券一张,多购多得,每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖200个,那么买100元商品中一等奖的概率应是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
9. 如图所示,一块直角三角形板ABC(![]() )的斜边AC与一个半径为1的圆轮子相靠,则CD等于( )
)的斜边AC与一个半径为1的圆轮子相靠,则CD等于( )
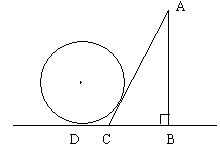
A. ![]() B.
B.
![]() C.
1
D.
C.
1
D. ![]()
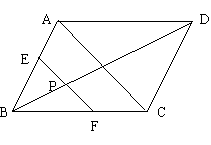
10. 如图所示,在平行四边形ABCD中,AC=4,BD=6,P是BD上任一点,过P作EF//AC,与平行四边形的两条边分别交于点E、F,设BP=,EF=![]() ,则能反映与
,则能反映与![]() 之间关系的图象为
之间关系的图象为
A. 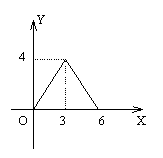 B.
B. 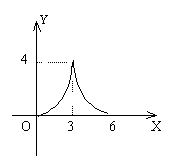
C. 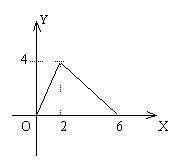 D.
D. 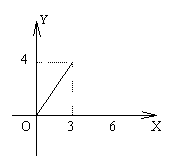
二. 填空题(每小题3分,共30分)
11. 计算:![]() .
.
12. 若![]() ,则
,则![]() .
.
13. 我国某城市有人口523800人,用科学计数法表示为 .
14. 已知![]() 是方程
是方程![]() 的两个实数根,则
的两个实数根,则![]() .
.
15. 如果两圆半径分别是2和3,圆心距是1,则两圆位置关系是 .
16. 抗“非典”期间,个别商贩将原来每桶价格![]() 元的过氧乙酸消毒液提高20%后出售,市政府及时采取措施,使每桶的价格在涨价后下降15%,那么现在每桶的价格是 元.
元的过氧乙酸消毒液提高20%后出售,市政府及时采取措施,使每桶的价格在涨价后下降15%,那么现在每桶的价格是 元.
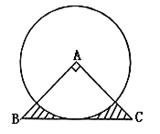
17. 如图所示,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ⊙A与BC相切,则图中阴影部分的面积为
.
⊙A与BC相切,则图中阴影部分的面积为
.
18. 给出下列程序:
(输入![]() )
)![]() (立方)
(立方)![]() (×k)
(×k)![]() (+b)
(+b)![]() (输出)
(输出)
且已知当输入的![]() 值为1时,输出值为1;输入的
值为1时,输出值为1;输入的![]() 值为-1时,输出值为-3.则当输入的
值为-1时,输出值为-3.则当输入的![]() 值为
值为![]() 时,输出值为 .
时,输出值为 .
19. 观察下列各式:
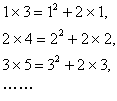
请你将猜想到规律用自然数![]() ,表示出来:
.
,表示出来:
.
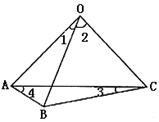
20. 如图所示,四边形OABC中,OA=OB=OC,![]() 是
是![]() 的4倍,若
的4倍,若![]() ,则
,则![]() .
.
三. 解答题(共60分)
21. (8分)计算:![]()
22. (8分)解方程:![]()
23. (10分)为防水患,在漓江上游修筑了防洪堤,其横截面为一梯形(如图所示),堤的上底宽AD和堤高DF都是6米,其中
(1)求证:![]()
(2)如果![]() ,求堤的下底BC的长。
,求堤的下底BC的长。
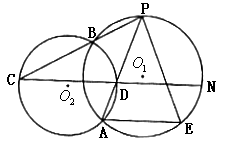
24. (10分)如图所示,已知⊙![]() 与⊙
与⊙![]() 相交于A、B两点,P是⊙
相交于A、B两点,P是⊙![]() 上一点,PB的延长线交⊙
上一点,PB的延长线交⊙![]() 于点C,PA交⊙
于点C,PA交⊙![]() 于点D,CD的延长线交⊙
于点D,CD的延长线交⊙![]() 于点N。
于点N。
(1)过点A作AE//CN交⊙![]() 于点E,求证:PA=PE
于点E,求证:PA=PE
(2)连结PN,若PB=4,BC=2,求PN的长。
25. (12分)某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同。安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生。
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低20%,安全检查规定,在紧急情况下全大楼的学生应在5分钟内通过4道门安全撤离,假设这栋教学大楼每间教室最多有45名学生。问:建造的这4道门是否符合安全规定?请说明理由。
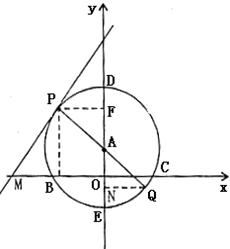
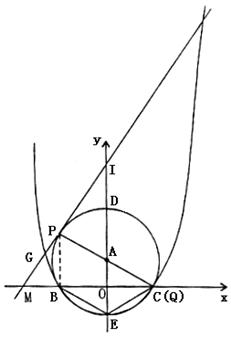
26. (12分)已知如图,点A在![]() 轴上,⊙A与
轴上,⊙A与![]() 轴交于B、C两点,与
轴交于B、C两点,与![]() 轴交于点D(0,3)和点E(0,-1)。
轴交于点D(0,3)和点E(0,-1)。
(1)求经过B、E、C三点的二次函数解析式;
(2)若经过第一、二、三象限的一动直线切⊙A于点P(s,t),与![]() 轴交于点M,连结PA并延长与⊙A交于点Q,设Q点的纵坐标为
轴交于点M,连结PA并延长与⊙A交于点Q,设Q点的纵坐标为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并观察图形写出自变量
的函数关系式,并观察图形写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)条件下,当![]() 时,求切线PM的解析式,并借助函数图像,求出(1)中抛物线在切线PM下方的点的横坐标
时,求切线PM的解析式,并借助函数图像,求出(1)中抛物线在切线PM下方的点的横坐标![]() 的取值范围。
的取值范围。
四. 选做题(共10分)
27. 已知如图,在![]() 中,AB=AC,
中,AB=AC,![]() ,BM=NM,BN=a,则点N到边BC的距离等于 。
,BM=NM,BN=a,则点N到边BC的距离等于 。
28. 已知关于![]() 的方程
的方程![]() 的两个实数根为
的两个实数根为![]() 、
、![]() ,且
,且![]() 。求证
。求证![]() 。
。

答案
一.1.B 2. C 3. D 4. C 5. A 6. C 7. C 8. A 9.D 10.A
二. 11. ![]() 12.
12. ![]() 13.
13. ![]() 4.
4.![]()
15. 内切 16. 1.02a 17. ![]() 18.
18.![]() 19.
19.![]()
20. ![]()
三.解答题
21. ![]()
22. ![]()
23. (1)略 (2)21米
24. (1)证明,连结AB,
![]() 四边形AEPB是⊙
四边形AEPB是⊙![]() 的内接四边形,
的内接四边形,
![]() 在⊙
在⊙![]() 中,
中,![]()
![]()
又![]() AE//CN,
AE//CN,
![]()
![]()
![]() 。
。
(2)连结AN,四边形ANPB是⊙![]() 的内接四边形,
的内接四边形,
![]()
![]() 由(1)可知
由(1)可知![]()
又![]() 。
。
又![]() 在⊙
在⊙![]() 中,由割线定理:
中,由割线定理:![]() ,
,
![]() .
.
25.解:(1)设平均每分钟一道正门可以通过![]() 名学生,一道侧门可以通过
名学生,一道侧门可以通过![]() 名学生,由题意得
名学生,由题意得
![]() 解得
解得 ![]()
答:平均每分钟一道正门可以通过学生120名,一道侧门可以通过学生80名。
(2)这栋楼最多有学生4×8×45=1440(名)。
拥挤时5分钟4道门能通过5×2(120+80)(1-20%)=1600(名)。
![]() ,
,
![]() 建造的4道门符合安全规定。
建造的4道门符合安全规定。
26. 解:
(1)![]() 为⊙A的直径,
为⊙A的直径,![]()
![]()
![]()
设经过B、E、C三点的抛物线的解析式为![]()
则![]() ,解得
,解得 ![]()
![]() 。
。
(2)过点P作PF⊥Y轴于F,过点Q作QN⊥Y轴于N。
![]() ,F点纵坐标为
,F点纵坐标为![]() ,
,
N点的纵坐标为![]()
![]()
![]()
![]()
![]() 动切线PM经过第一、二、三象限,观察图形可得
动切线PM经过第一、二、三象限,观察图形可得![]()
![]()
![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]()
(3)当![]() 时,Q点与C点重合,连结PB。
时,Q点与C点重合,连结PB。
![]() 为⊙A的直径,
为⊙A的直径,![]() ,即PB⊥
,即PB⊥![]() 轴。
轴。
![]() 将
将![]() 代入
代入![]()
得 ![]()
设切线PM与![]() 轴交于点I,则AP⊥PI
轴交于点I,则AP⊥PI
![]()
在![]() 与
与![]() 中,
中,
![]()
![]()
![]()
![]() 点坐标为(0,5),设切线PM的解析式为
点坐标为(0,5),设切线PM的解析式为
![]()
![]() 点的坐标为
点的坐标为![]() 解得
解得![]()
![]() 切线PM的解析式为
切线PM的解析式为![]() 设切线PM与抛物线
设切线PM与抛物线![]() 交于G、H两点,由
交于G、H两点,由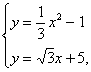 可得
可得 ![]()
因此,G、H的横坐标分别为![]() 、
、![]() 。根据图象可得抛物线在切线PM下方的点的横坐标
。根据图象可得抛物线在切线PM下方的点的横坐标![]() 的取值范围是
的取值范围是![]()
27. 设![]()
设为![]() ,作ND⊥BC于D,在
,作ND⊥BC于D,在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
![]()
28. 只要证![]() 即可。
即可。
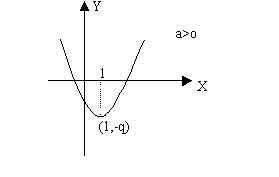
法二:![]() 的抛物线,当
的抛物线,当![]() 时,
时,
相应的![]() 值为:
值为:![]()
![]() 抛物线的顶点
抛物线的顶点![]() 必在
必在![]() 轴或
轴或![]() 轴的下方。
轴的下方。
而抛物线的开口向上,
![]() 抛物线与
抛物线与![]() 轴的两交点必在1的两侧或同在1这个点。
轴的两交点必在1的两侧或同在1这个点。
![]()