初三数学阶段测试题
（范围：分式及一元二次方程 答卷时间：120分钟 满分:150分）
一、填空题（本题共８小题，每题3分，共2４分）
1．
分式
有意义，则x
．
2．
分式
的值是0，则
．
3．
2003年4月16日世界卫生组织宣布：冠状病毒的一个变种是引起“非典”的病原体，某种冠状病毒的直径约为120纳米，1纳米=
，则这种冠状病毒的直径用科学记数法表示为
米．
4．
已知关于X的方程
的一根是1，则另一根为 ，ｍ＝ ．
5． 写出以2，－3为根的一元二次方程为 。
6．
若关于x的方程
有增根，则增根是
，m=
．
7． 写出一个关于x的方程满足：有一个根是－1，一次项系数是－5 ．
8．
用配方法解方程
，可将原方程化为 的形式．
二、选择题（本题共７小题，每题３分，共２１分）
9．下列计算正确的是 （ ）
Ａ：
Ｂ：
Ｃ：
Ｄ：
10．关于x的方程
的根的情况是
（ ）
A：有两个不相等的实数根 B：有两个相等的实数根 C：没有实数根 D：不确定
11．与
相等的是 （ ）
Ａ：
Ｂ：
Ｃ：
（ｘ≠ｙ） Ｄ：
12．x g盐溶解在a g水中，取这种盐水m g，其中含盐 （ ）
A：
B：
C：
D：
13．方程
是关于ｘ的一元二次方程，则ｍ （ ）
Ａ：ｍ≠０ Ｂ：ｍ≠１ Ｃ：ｍ≠－１ Ｄ：ｍ≠±１
14．若一元二次方程
无实根，则一次函数y=（m+1）x+m－1的图象不经过（ ）
A：第一象限 B：第二象限 C：第三象限 D：第四象限
15．下列是某同学在一次测验中解答的填空题：
（1）
若
，则ｘ＝ａ;
（2） 方程2ｘ（ｘ－１）＝（ｘ－１）的解为ｘ＝０;
（3）
方程
的两根之和为 ２ ;
其中答案完全正确的题目个数为 （ ）
Ａ：０个 Ｂ：１个 Ｃ：２个 Ｄ：３个
三、解答题（本题共６小题，１６－１９题各９分，２０题１０分，２１题１２分，共５８分）
16．
１７．(－2x2)5÷(－x3)2－(2x)4
１８．
１９．
20．m取何值时，关于x的方程
有两个相等的实数根；并求出这时方程的根。
２1．某少年军校的师生到距学校15km的部队营地参观学习。一部分人骑自行车走，过了40分钟，其余的人乘汽车出发，结果他们同时到达。已知汽车的速度是自行车的3倍，求两车的速度。
四．解答题（本题共２小题，各８分，共１６分）
22．美化环境，改善人民的居住环境已经成为城市建设的一项重要内容，金州区近几年来，通过拆迁旧房，植草，栽树，修建公园等措施，使城市绿地面积不断增加，如图所示
（1）根据如图提供的信息，回答下列问题。2003年底绿
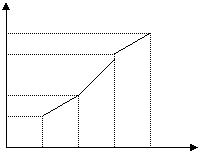绿地面积（公顷）
地面积为
公顷；比2002年底增加了
60 公顷，在2001年，2002年，2003年这三年中，绿地面积增
56 加最多的是 年；
（2）为满足城市发展的需要，计划到2005年年底使城区
51 绿地总面积达到72．6 公顷,试求今明两年绿地面积的年平均
48 增长率。
2000 2001 2002 2003年份
城区每年年底绿地面积统计图
23．设
是关于x的方程
的两个根，且满足
，求m的值。
五．阅读题（本题共２小题，２４题１２分，２５题８分，共２０分）
24．观察下列各式：
．．．
（１）由此可以推测
；
（２）请猜想出能表示（１）的特点的一般规律,用含字母m的等式表示出来，并说明理由
（M表示整数） ；
（３）请直接用（２）中的规律计算：
25．阅读材料后解决问题.
一般地,我们把形如
的多项式叫做关于x的二次三项式．令二次三项式的值等于０，得到的就是该二次三项式对应的一元二次方程，二次三项式的因式分解与一元二次方程有着密切的联系．一方面，利用因式分解可以解一元二次方程；另一方面，利用解一元二次方程，可以分解二次三项式．
设一元二次方程
的两个根为
，
，由根与系数的关系可知：
也就是说
．
而
这说明，在分解二次三项式
时，可先求出对应方程的两个根
，然后写成
．
请将下列各式在实数范围内分解因式：
（１）
（２）
六．解答题（１１分）
26．有一块长4米，宽3米的空地，现要在空地上建一花坛，使花坛的面积是原空地面积的一半，如何设计？请设计四种方案，并在你设计的方案中任选一种，作简单说明。（多设计一种加２分，加到４分为止）
答案：
一．
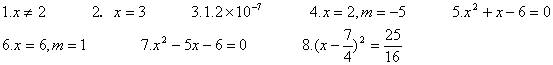
二．
９．Ｄ １０．Ａ １１．Ｃ １２．Ｄ １３．Ｂ １４．Ａ １５．Ａ
三．
四．
２２．（１）６０ ４ ２００２ （２）增长率为１０％
２３．（１）ｍ＝１５
五．
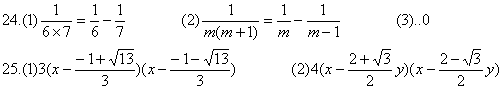
六．（略）