初三数学竞赛试卷

初三数学竞赛试卷

题　号	一		二		三		总　分
	1~8	9~14	15	16	17	18
得　分

一、选择题(共8小题，每小题5分，满分40分. 以下每小题均给出了代号为A、B、C、D的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填均得零分)

　　1．如果，那么代数式m是　　　　　　　　　  （　 ）

　　（A）　 （B）　　（C）　 （D）　

2．在平面直角坐标系中，点A（，）在第四象限，那么点

B（，）在　　　　　　　　　　　　　　　　　　　　　　  （　 ）

（A）第一象限　 （B）第二象限　 （C）第三象限 　（D）第四象限

3．如图，以数轴的单位长线段为边作一个正方形，以数轴的原点为圆心 ，正方形的对角线长为半径画弧，交数轴于点A，点A表示数x，则x²的平方根是　　　 　　　　　　　　　　　　　　　　　　　　　　　　　（　 ）

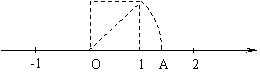（A） 　　 （B）　

（C）　 　　 （D）2

4．如果，那么等于　　　　　　　　　  (　　)

（A）4　　（B）3 　 （C）2　　（D）1

	初中数学竞赛试卷　第1页(共6页)

5．考虑下列4个命题：

　　①有一个角是100°的两个等腰三角形相似；

　　②斜边和周长对应相等的两个直角三角形全等；

　　③对角线互相垂直且相等的四边形是正方形；　　

　　④对角线相等的梯形是等腰梯形．

　　其中正确命题的序号是　　　　　　　　　　　　　　　　　　 (　　)

(A)①②③④　　(B)①②④　　　(C)②③④　　(D)①④

6．已知如图，在矩形ABCD中有两个一条边长为1的平行四边形.则它们的公共部分(即阴影部分)的面积是　　　　　　　　　　　　　　　  (　　 )

（A）大于1　

（B）等于1

（C）小于1　

（D）小于或等于1

7．已知梯形的两条对角线分别为m与n，两对角线的夹角为60　　　 ⁰. 那么，该梯形的面积为　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

（A）　　 （B）　　 （C）　　 （D）

8．已知，正整数n，k满足不等式，那么当n与k取最小值时，n+k的值为　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

（A）29　　　　 （B）30　　　　 （C）31　　　　　 （D）32

二、填空题（共6小题，每小题5分，满分30分）

9．已知⊙O的直径AB=2cm，过点A有两条弦AC=2cm，AD=cm，那么劣弧CD 的度数为_________.

初中数学竞赛试卷　第2页(共6页)

10．已知，关于x的一元二次方程与只有一个公共的根，那么方程所有的根的和是　　　　  .

11．在写有整式 ，，，，，，，的卡片中，任意选取其中两张分别作为分子和分母，得到一个分式的概率是　　　　.

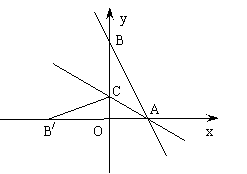12．如图，直线与x轴、

y轴分别交于A点和B点，C是OB上的一

点，若将DABC沿AC翻折得到DAB^/C，B^/

落在x轴上，则过A，C两点的直线的解析

式是　　　　　　  .

13．若，则=　　　.　

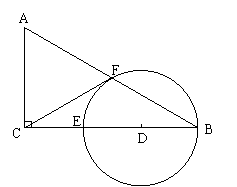
14．如图，在DABC中，ÐC=90°，D、E

分别是BC上的两个三等分点，以D为圆心的

圆过点E，且交AB于点F，此时CF恰好与

⊙D相切于点F. 如果AC=，那么⊙D的半

径=　　　　.

三、解答题（共4题，分值依次为12分、12分、12分、14分，满分50分）

15．已知，一次函数（是不为0的自然数，且是常数）的图象与两坐标轴所围成的图形的面积为（即k=1时，得，k=2时，得，┅）.试求+++的值.

	初中数学竞赛试卷　第3页(共6页)

16．一商店销售某种食品，每天从食品厂批发进货，当天销售. 已知进价为每千克5元，售价为每千克9元，当天售不出的食品可以按每千克3元的价格退还给食品厂. 根据以往销售统计，该商店平均一个月(按30天计算)中，有12天每天可以售出这种食品100千克，有18天每天只能售出60千克. 食品厂要求商店每天批进这种食品的数量相同，那么该商店每天从食品厂批进这种食品多少千克，才能使每月获得的利润最大?最大利润是多少?

初中数学竞赛试卷　第4页(共6页)

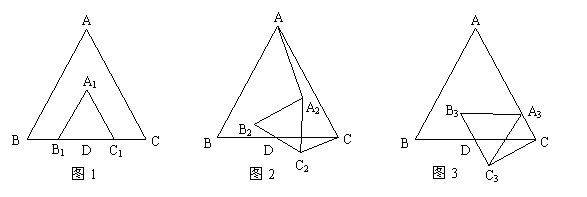
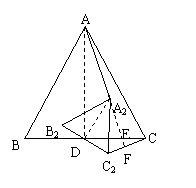
17．已知，∆ABC和∆A₁B₁C₁均为正三角形，BC和B₁C₁的中点均为D，如图1.

　　 (1)当∆A₁B₁C₁绕点D旋转到∆A₂B₂C₂时，试判断AA₂与CC₂的位置关系，并证明你的结论.

　　 (2)如果当∆A₁B₁C₁绕点D旋转一周，顶点A₁和AC仅有一个交点，设该交点为A₃，如图3. 当AB=4时，求多边形ABDC₃C的面积.

		初中数学竞赛试卷　第5页(共6页)

　　18．给出一个三位数. 重排这个三位数三个数位上的数字，得到一个最大的数和一个最小的数，它们的差构成一个三位数（允许百位数字为零），再重排这个得到的三位数三个数位上的数字，又得到一个最大的数和一个最小的数，它们的差又构成另一个三位数（允许百位数字为零），重复以上过程.　问重复2007次后所得的数是多少？证明你的结论.

初三数学竞赛参考答案和评分意见

　　　　　　　　　　　　　　　　　　　　

一、选择题(每小题5分，共40分)

1—8：ACAD  BCBC

二、填空题(每小题5分，共30分)

9． 30°或150°　 10． 0　　11．　　12． 　 13．1　　 14．　

三、解答题（共4题，分值依次为12分、12分、12分、14分，满分50分）

15．一次函数的图象与两坐标轴的交点为（，0）、（0，），

所围成的图形的面积为.　　　…………4分

∴+++

=　 …………8分

=

=

=

=.　　　　　　　　　　　　　　　　　　　 …………12分

16．设该商店每天批进这种食品x千克，每月获得的利润为y元．

（1）当时，由题意，30天中批进这种食品的成本为元，销售收入为元，退货所得为元，

于是可得　

即　　　　　　　　　　　　　　　　　　  …………4分

∵是一次函数，且y随x的增大而增大，

∴当时，即每天批进这种食品100千克时，可获得最大利润，最大利润为7680元．　　　　　　　　　　　　　　　　　　　　　　　  …………8分

（2）当时，由题意，

化简得

∵是一次函数，且y随x的增大而减小，

∴当时，即每天批进这种食品100千克时，可获得最大利润，最大利润为7680元．　　　　　　　　　　　　　　　　　　　　　　　  …………12分

17．AA₂⊥CC₂.　　　　　　　　　　　 　…………2分

（1）在图2中，连接AD、A₂D、延长AA₂

交BC于E，交CC₂于F，

∵ÐADA₂=90°-ÐA₂DC=ÐCDC₂，

（等边三角形都相似，相似三角形对应高的比等于相似比）

∴DAA₂D∽DCC₂D，于是得ÐA₂AD=ÐC₂CD　　　…………5分

又因为ÐAED=ÐCEF，∴ÐADE=ÐCFE=90°

　  ∴AA₂⊥CC₂.　　　 　　　　　　　　　　…………8分

（2）在图3中，连接A₃D，过C₃作C₃G⊥BC于G，由（1）得AC⊥CC₃，

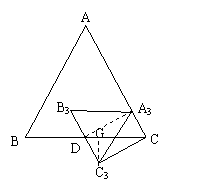由题意又得A₃D⊥AC，

　  四边形A₃CC₃D是矩形.

　  ∴C₃C=A₃D=，

　  C₃G=，

　  ∴多边形ABDC₃C的面积=

　　　 ==.　　　　　 …………12分

　　 18．经过2007步后得到495或0.　　　　　　　　　　　 …………2分

不妨设选定的三位数中的最大数字为，最小数字为，还有一个数字为，则，　　　　  …………4分　

现讨论如下：

（1），，第一步结果0.

　（2），，第一步结果099,第二步结果891,第三步结果792 ,第四步结果693，第五步结果954,第六步结果495.

　（3），，第一步结果198，第二步结果792，第三步结果692，第四步结果954，第五步结果495.

　（4），，第一步结果297,第二步结果693,第三步结果954 ,第四步结果495.

　（5），，第一步结果396,第二步结果594,第三步结果495.

　（6），，第一步结果495.

　（7），，第一步结果594,第二步结果495.

　（8），，第一步结果693，第二步结果594，第三步结果495.

　（9），，第一步结果792 ,第二步结果693,第三步结果954,第四步结果495.

　（10），，第一步结果891,第二步结果792 ,第三步结果693,第四步结果954,第五步结果495. 

由以上讨论可知至多6步可将一个三位数变为495或0，然后就进入循环，所以经过2007步后将得到495或0.

当时，得到0；当时，得到495.　 …………14分（讨论一种情况给1分）

	初中数学竞赛试卷　第6页(共6页)