第四章 相似三角形复习
一、比例线段：
`1.比例的基本性质：ad＝bc
2.黄金分割：如图点P把线段AB分成两条线段AP和PB，若
，那么称线段AB被点P黄金分割。线段AP与AB的比叫
，
.
练习：
1、已知ab＝cd，请写出有关a，b，c，d成立的比例式。（至少六个）
2、如图，点A,B是反比例函数
图像上的两点，请写出关于图中的四条线段a，b，c，d的一个比例式
3、已知3x=4y，则
= （ ）
A、
B、
C、
D、以上都不对
4、已知点C是AB的黄金分割点，且AC>BC,则
，
.
5、下列各组中得四条线段成比列得是（ ）
A、4cm、2cm、1cm、3cm B、1cm、2cm、3cm、4cm
C、25cm、35cm、45cm、55cm D、1cm、2cm、20cm、40cm
6、若x是3和6的比例中项，则x的值为 （ ）
A、
B、
C、
D、
7、若P是线段AB的黄金分割点（PA＞PB），设AB=1，则PA的长约为 （ ）
A、0.191 B、0.382 C、0.5 D、0.618
8、在比例尺为1：的“中国政区”地图上，量得甲市与乙市之间的距离是6.5cm，则这两市之间的实际距离为 km；
9、已知：x∶y∶z=2∶3∶4，则
的值为 。
10、已知线段AB，用直尺和圆规求作这条线段的黄金分割点P。
二、相似三角形：
1、相似三角形的判定方法：
a、 定义：对应角相等，对应边成比例的两个三角形相似
b、预备定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。
C、 对应相等的两个三角形相似。
D、两边 ，且 相等的两个三角形相似。
E、三边 ，两个三角形相似。
2、相似三角形的性质：
a、相似三角形 相等。
b、相似三角形 成比例。
c、相似三角形的周长之比等于 ；
d、相似三角形的面积之比等于 。
e、相似三角形的对应高线、中线、角平分线之比等于 。
练习：
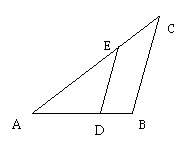
1、下面两个三角形相似吗?为什么?
 | |||
 | |||
(1)DE ∥BC (2)
(3) (4)
2、
如图判断4×4方格中的两个三角形是否相似,并说明理由.
 |
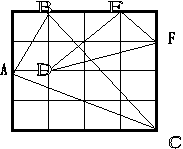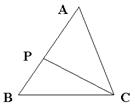
3.如图,P是△ABC中AB边上的一点,要使△ACP∽△ABC需添加一个条件为___________ .
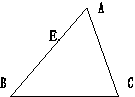
4、已知, △ABC∽△DEF,相似比为2,那么他们的周长之比为 ，面积之比为 .
5、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2, 在AC上取一点F,使以A、E、F为顶点的三角形与 △ABC相似,那么AF=________.
6、若△ABC∽△A′B′C′，且
，△ABC的周长为12cm，则△A′B′C′的周长为
；
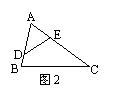
7、如图1，在△ABC中，中线BE、CD相交于点G，则
= ；S△GED：S△GBC= ；
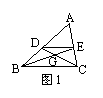
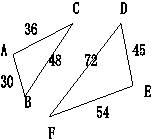
8、如图2，在△ABC中， ∠B=∠AED，AB=5，AD=3，CE=6，则AE=
；
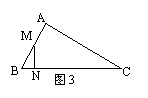
5、如图3，△ABC中，M是AB的中点，N在BC上，BC=2AB，∠BMN=∠C，则△ ∽△
，相似比为
，
=
；
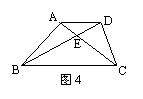
6、如图4，在梯形ABCD中，AD∥BC，S△ADE：S△BCE=4：9，则S△ABD：S△ABC= ；
7、两个相似三角形的周长分别为5cm和16cm，则它们的对应角的平分线的比为 ；
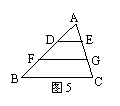
8、如图5，在△ABC中，BC=12cm，点D、F是AB的三等分点，点E、G是AC的三等分点，则DE+FG+BC= ；
9、已知，如图，在△ABC中，∠C=600，AD⊥BC于D，BE⊥AC于E，试说明△CDE∽△CBA。
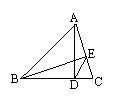
10、
如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块 矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上,且矩形的面积是三角形面积的一半,求这个矩形的长和宽各是多少?
 |
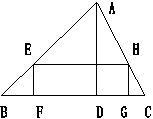1、
2、