|
一．填空题
1．已知三个数1，
，5，请再添一个数，使它们构成一个比例式，则这个数可以是 ．
2．已知
＝4，
＝9，
是
的比例中项，则＝ ．
3．若
，则
；若
，则
∶
＝ ．
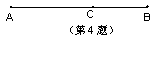
4．如右图，点C是线段AB的黄金分割点（AC＞BC），请写出一个比例式 ，如果AB＝1cm，则AC＝ cm，BC＝ cm．
5．一本书的长与宽之比为黄金比，若它的长为20cm，则它的宽是 cm（保留根号）．
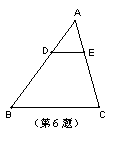
6．如图，在ΔABC中，DE∥BC，且AD∶BD＝1∶2，则
．
若梯形DBEC的面积是32
，则ΔABC的面积是 ．
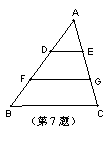
7．如图，在ΔABC中，DE∥FG∥BC，且AD＝DE＝EF，则
．
 |  | ||||||
 | |||||||
| |||||||
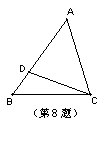
8．如图，要使ΔABC∽ΔACD，从边的角度，需补充的条件是 ．
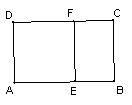
9．如图，矩形ABCD∽矩形BCFE，且AD＝AE，则AB∶AD＝ ．
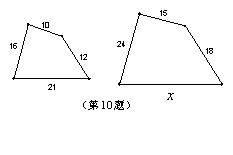
10．如图，若两个多边形相似，则
＝ ．
11．一公园占地面积约为800000
，若按比例尺1∶2000缩小后，其面积约为 ．
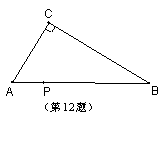
12．如图，点P是RtΔABC斜边AB上的任意一点（A、B两点除外）过点P作一条直线，使截得的三角形与RtΔABC相似，这样的直线可以作 条．
13．据科学测定，当气温处于人体正常气体温的黄金比时，人体感到最舒适，这个气温约为
（精度到1摄氏度）．
14．已知ΔABC∽ΔA′B′C′，且BC∶B′C′＝AC∶A′C′，若AC＝1，A′C′＝2，则ΔA′B′C′与ΔABC的相似比是 ．
15．已知ΔABC∽ΔA′B′C′，ΔABC的周长是20cm，ΔA′B′C′的周长是12cm，ΔABC的最长边为8cm，则ΔA′B′C′的最长边是 cm．
16．如图，P是ΔABC的边AB上一点，若ΔAPC∽ΔABC，，则∠1＝∠ ．
17．在ΔABC中，AB＝4，BC＝9，AC＝8，在AC上取一点M，当AM的长为 时，
ΔAMB∽ΔABC．
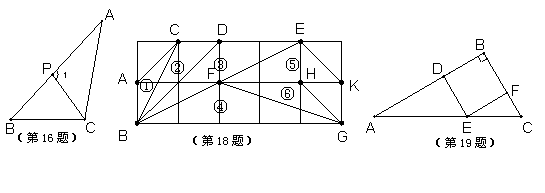18．如图，在正方形网格上有6个三角形：ΔABC；②ΔCDB；③ΔDEB；④ΔFBG；⑤ΔHGF；⑥ΔEKF，在②─⑥中，与①相似的三角形的是 （填序号）．
19．如图，四边形BDEF是RtΔABC的内接正方形，若AB＝6，BC＝4，则DE＝ ．
20．已知三个边长分别为2，3，5的正方形如图排列，则图中阴影部分的面积是 ．
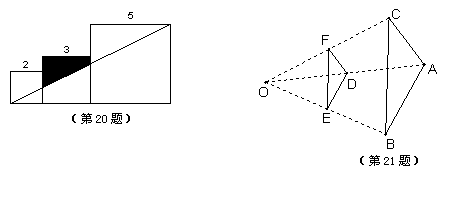21．如图，ΔABC与ΔDEF是位似三角形，且AC＝2DF，则OE∶OB＝ ．
二、选择题
1．下列各组数中，成比例的是（ ）
A．－6，－8，3，4 B．－7，－5，14，5 C．3，5，9，12 D．2，3，6，12
2．下列三角形中，一定相似的是（ ）
A．两个等腰三角形 B．两个直角三角形 C．两个等边三角形 D．两个钝角三角形
3．若是和
的比例中项，则关于
的一元二次方程
的根的
情况是（ ）
A．有两个相等实数根 B．有两个不相等[实数根 C．没有实数根 D．无法判断
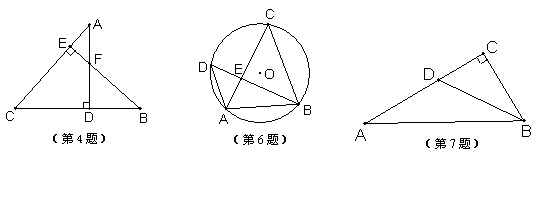
4．如图，AD⊥BC于点D，BE⊥AC于点E，则图中相似三角形的对数是（ ）
A．3对 B．4对 C．5对 D．6对
5．下列说法中不正确的是（ ）
A．有一个角是30°的两个等腰三角形相似；B．有一个角是60°的两个等腰三角形相似；
C．有一个角是90°的两个等腰三角形相似；D．有一个角是120°的两个等腰三角形相似；
6．如图，已知ΔABC和ΔABD都是⊙O的内接三角形，AC和BD相交于点E，则与ΔADE相似的三角形是（ ）
A．ΔBCE B．ΔABC C．ΔABD D．ΔABE
7．如图，RtΔABC中，∠C＝90°，D是AC边上一点，AB＝5，AC＝4，若ΔABC∽ΔBDC，
则CD＝ ．
A．2 B．
C．
D．
8．两个相似多边形的面积之比为1∶3，则它们周长之比为（ ）
A．1∶3 B．1∶9 C．1∶
D．2∶3
三、作图题
1．如图，已知线段AB，用直尺和圆规作出它的黄金分割点（写出作法，并保留作图痕迹）．
2．如图，已知ΔABC和点O，以点O为位似中心，求作ΔABC的位似图形ΔA′B′C′，并把
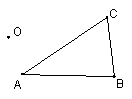ΔABC的边长缩小到原来的
．
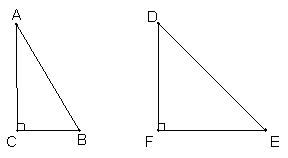
3．已知：如图，RtΔAB中，∠C＝90°，∠A＝30°，RtΔDEF中，∠F＝90°，DF＝EF，能否分别将这两个三角形各分割成两个三角形，使ΔABC所分成的每个三角形与ΔDEF分成的每个三角形分别对应相似．若能，请设计出一种分割方案；若不能，请说明理由．
四．解答题．
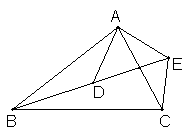
1．如图，
．
求证：（1）∠BAD＝∠CAE． （2）ΔABD∽ΔACE．
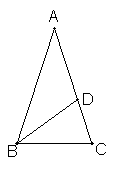
3．如图，在ΔABC中，AB＝AC，∠A＝36°，BD是角平分线．
求证：（1）ΔABC∽ΔBCD； （2）BC是CD与CA的比例中项．