中考数学模拟二
考生注意:本卷共八大题,计23小题,满分150分,考试时间120分钟.
一、选择题(本题共10小题,每小题4分,满分40分)
1.︱-32︱的值是 ( )
A、-3 B、3 C、9 D、-9
2.为了迎接2008年奥运会在中国北京举行,北京市现在执行严格的机动车尾汽排放标准,同时正在设法减少工业及民用燃料所造成的污染,随着每年10亿立方米的天然气输送到北京,到2007年底,空气质量将会基本达到发达国家城市水平,10亿用科学记数法可以表示为 ( )
(A) 1.0×10![]() (B) 1.0×10
(B) 1.0×10![]() (C) 1.0×10
(C) 1.0×10![]() (D) 1.0×10
(D) 1.0×10![]()
3.、下列计算中,正确的是 ( )
A、X3+X3=X6 B、a6÷a2=a3 C、3a+5b=8ab D、(—ab)3=-a3b3
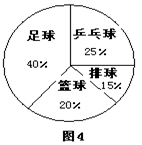 4.某校九(3)班的全体同学喜欢的球类运动用图4所示的统计图来表示,下面说法正确的是
( )
4.某校九(3)班的全体同学喜欢的球类运动用图4所示的统计图来表示,下面说法正确的是
( )
A、从图中可以直接看出喜欢各种球类的具体人数;
B、从图中可以直接看出全班的总人数;
C、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况;
D、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系。
5.下列结论正确的个数是 ( )
(1)一个多边形的内角和是外角和的3倍,则这个多边形是六边形
 (2)如果一个三角形的三边长分别为6、8、10,则最长边上的中线长为5
(2)如果一个三角形的三边长分别为6、8、10,则最长边上的中线长为5
(4)若等腰三角形有一个角为80°,则底角为80°或50°
A. 1 B. 2 C. 3 D. 4
6.关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根为0 ,则a的值为 ( )
A 1 B -1 C 1或-1 D 都不对
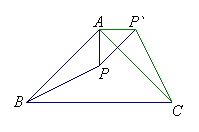
7.如图ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于 ( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.点M(-sin60°,cos60°)关于x轴对称的点的坐标是 ( )
A.(![]() )
B.(-
)
B.(-![]() )
C.(-
)
C.(-![]() ,
,![]() ) D.(-
) D.(-![]() ,-
,-![]() )
)
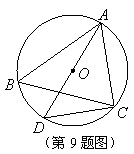
9.如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,连接
的直径,连接![]() ,若
,若![]() 的半径
的半径![]() ,
,![]() ,则
,则![]() 的值是
( )
的值是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
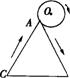 10.如右图,一个等边三角形的边长和与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了
( )
10.如右图,一个等边三角形的边长和与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了
( )
A.4圈 B.3圈 C.5圈 D.3.5圈
二、填空题(本题共4小题,每小题5分,满分20分)
11.分解因式![]() =
.
=
.
12.请选择一组你喜欢的![]() 的值,使二次函数
的值,使二次函数![]()
![]() 的图象同时满足下列条件:①开口向下,②当
的图象同时满足下列条件:①开口向下,②当![]() 时,
时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() 时,
时,![]() 随
随![]() 的增大而减小.这样的二次函数的解析式可以是 .
的增大而减小.这样的二次函数的解析式可以是 .
13.己知:如图,菱形ABCD中,∠B=600,AB=4,则以AC为边长的正方形ACEF的周长为 .
14.如下图,某同学从A点出发前进10米,向右转18°,再前进10米,又向右转18°,这样下去,他第一次回到出发点A时,一共走了______米。
三、(本题共2小题,每小题8分,满分16分)
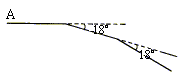
 15.计算:
15.计算: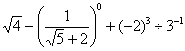
【解】
16.解方程![]()
【解】
四、(本题共2小题,每小题8分,满分16分)
17.已知圆锥的底面半径为r=20cm,高h=![]() cm,现在有一只蚂蚁从底边上一点A出发。在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离。
cm,现在有一只蚂蚁从底边上一点A出发。在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离。
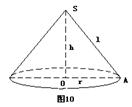 【解】
【解】
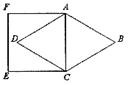
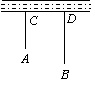 18.如图,一牧童在A处牧马,牧童家在B处,A,B处距河岸的距离AC,BD分别为500m和700m,且CD=500m,天黑前牧童从A处将马赶到河边去饮水后再回家,请你帮牧童求出他最少要走多少米?
18.如图,一牧童在A处牧马,牧童家在B处,A,B处距河岸的距离AC,BD分别为500m和700m,且CD=500m,天黑前牧童从A处将马赶到河边去饮水后再回家,请你帮牧童求出他最少要走多少米?
【解】
五、(本题共2小题,每小题10分,满分20分)
19.某电视台的娱乐节目有这样的翻奖游戏,正面为数字,背面写有祝福语或奖金数,如下面的表格.游戏的规则是:参加游戏的人可随意翻动一个数字牌,看背面对应的内容,就可以知道是得奖还是得到祝福语.
 |
(1)写出“翻到奖金1000元”的概率;
(2)写出“翻到奖金”的概率;
(3)写出“翻不到奖金”的概率.
【解】
20.观察右表中数字的排列规律,回答下面
| 1 | 3 | 5 | 7 | … |
| 2 | 6 | 10 | 14 | … |
| 4 | 12 | 20 | 28 | … |
| 8 | 24 | 40 | 56 | … |
| … | … | … | … | … |
的问题
①表中第1行第5列的数字是 ;
②表中第5行第4列的数字是 ;
③请用关于n的代数式表示表中第3列
第n行的数为 ;
④明年将在我国举行奥运盛会,那么你知道数字2008的位置是第 行,第 列.
六、(本题满分12分)
21.某商店经营一批进价为2元的小商品,在市场营销的过程中发现:如果该商品按最低价3元销售,日销售量为18件,如果单价每提高1元,日销售量就减少2件.设销售单价为x(元),日销售量为y(件).
(1)写出日销售量y(件)与销售单价x(元)之间的函数关系式;
(2)设日销售的毛利润(毛利润=销售总额-总进价)为P(元),写出毛利润P(元)与销售单价x(元)之间的函数关系式;
(3)在图所示的坐标系中画出P关于x的函数图象的草图,并标出顶点的坐标;
(4)观察图象,说出当销售单价为多少时,日销售的毛利润最高?是多少?
 【解】
【解】
七、(本题满分12分)
22.阅读与理解:
图22—1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和CDE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连结AD,BE,如图22—2;
在图22—2中,线段BE与AD之间具有怎样的大小关系?证明你的结论.
(2)操作:若将图22—1中的△C′DE,绕点C按顺时针方向任意旋转一个角度![]() ,连结AD,BE,如图22—3;
,连结AD,BE,如图22—3;
在图22—3中,线段BE与AD之间具有怎样的大小关系?证明你的结论.
猜想与发现:
根据上面的操作过程,请你猜想当![]() 为多少度时,线段AD的长度最大?是多少?当
为多少度时,线段AD的长度最大?是多少?当![]() 为多少度时,线段AD的长度最小?是多少?
为多少度时,线段AD的长度最小?是多少?
 A
A
A
A
A
A
DDD
八、(本题满分14分)
23.如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连结MP.已知动点运动了t秒.
(1)P点的坐标为( , )(用含t的代数式表示);
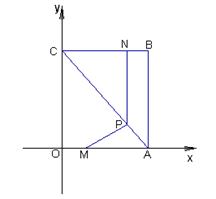 (2)试求
△MPA面积的最大值,并求此时t的值;
(2)试求
△MPA面积的最大值,并求此时t的值;
(3)请你探索: 当t为何值时,△MPA是一个等腰三角形?
答案
选择题
1,C 2,B 3,D 4,D 5,B 6,B 7,C 8,B 9,B 10,A
填空题
1,X(X—Y+1)(X—Y—1) 2,Y=--(X—2)![]() 3,16 4,200
3,16 4,200
三、(本题共2小题,每小题8分,满分16分)
15, --23
16,![]() X=2
X=2
四、(本题共2小题,每小题8分,满分16分)
17,![]() 80
80![]()
18,1300
五、(本题共2小题,每小题10分,满分20分)
19,![]()
![]()
![]()
20, 9 112
5×2![]()
4 126
六、(本题满分12分
21,1,y=24-2x
2,p=(x-2)(24-2x)
3,略
4, 7 50
七、(本题满分12分)
解:操作与证明:
(1)BE=AD.……………………………………………………………………(1分)
∵△C′DE绕点C按顺时针方向旋转30°,∴∠BCE=∠ACD=30°.
∵△ABC与△C′DE是等边三角形,∴CA=CB,CE=CD.
∴△BCE≌△ACD.∴BE=AD.…………………………………………(3分)
(2)BE=AD.……………………………………………………………………(4分)
∵△C′DE绕点C按顺时针方向旋转的角度为![]() ,∴∠BCE=∠ACD=
,∴∠BCE=∠ACD=![]() .
.
∵△ABC与△C′DE是等边三角形,∴CA=CB,CE=CD.
∴△BCE≌△ACD.∴BE=AD.…………………………………………(6分)
猜想与发现:
当![]() 为180°时,线段AD的长度最大,等于a+b;当
为180°时,线段AD的长度最大,等于a+b;当![]() 为0°(或360°)时,线段AD的长度最小,等于a -b.………………………………………………(8分)
为0°(或360°)时,线段AD的长度最小,等于a -b.………………………………………………(8分)
八、(本题满分14分)
解:(1)(6—t, t ) …… 2分
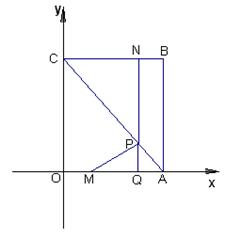
(2)延长NP交x轴于Q,则有PQ⊥QA. 设△MPA的面积为S
S= MA·PQ …… 3分
=(6—t)t
=—t2+4t (0≤t≤6) …… 5分
∴当t =3时,S的最大值为6 …… 7分
(3) ① 若MP=PA
∵PQ⊥MA
∴ MQ=QA=t
∴3t=6 即t=2 ……8分
② 若MP=MA
则 MQ=6—2t PQ=t
PM=MA=6—t
在Rt△PMQ 中
∵PM2=MQ2+PQ2
∴(6—t)=(6—2t)+(t)
∴t =![]() …… 10分
…… 10分
③ 若PA=AM
∵PA=t AM=6—t
∴t=6—t
∴t= …… 11分
 综上所述, t=2或t= 或t=
…… 12分
综上所述, t=2或t= 或t=
…… 12分