九年级数学试题
本试卷1～8页，共150分，考试时间120分钟。
请考生准备好圆规，直尺、三角板、计算器等答题工具，祝愿所有考生都能发挥最佳水平。
一、选择题(本题8小题，每小题3分，共24分)
说明:将下列各题唯一正确的答案代号A、B、C、D填到题后的括号内。
1.－
的倒数是 ( )
A.
B.－ C.
D.－
2. 下列成语所描述的事件是必然事件的是( )
A．水中捞月 B．拔苗助长 C．守株待兔 D．瓮中捉鳖
3.半径为5和2的两圆相内切，则其圆心距为 ( )
A.2 B.3 C.5 D.7
4.下列各式运算正确的是( )
A.
B.
C.
D.
5. 一个全透明的玻璃正方体，上面嵌有一根黑色的金属丝，如图，金属丝在俯视图中的形状是( )
6．二次函数的图象向右平移3个单位，得到
，则原来的图象的函数表达式是( )
(A)
(B)
(C)
(D)
7. 下列四个几何体中，正视图、左视图与俯视图是全等图形的几何体是（ ）
(A)圆柱 (B)圆锥 (C)三棱锥 (D)球
8．小明根据邻居家的故事写了一首小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还。”如果用纵轴
表示父亲与儿子行进中离家的距离，用横轴
表示父亲离家的时间，那么下面的图象与上述诗的含义大致吻合的是（
）
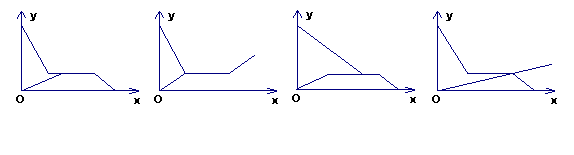
（A） （B） （C） （D）
二、填空题(本题共7小题，每小题3分，共21分)
说明：将答案直接填在题后的横线上。
9.一只口袋里有相同的红、绿、蓝三种颜色的小球，其中有4个红球，5个绿球．若任意摸出一个绿球的概率是
，则任意摸出一个蓝球的概率是 ．
10.反比例函数
的图象过点A(－3，
)，则k的值为____________；
11.在Rt△ABC中，∠C=90°，AC = 2，BC =5，则tanA的值为______________；
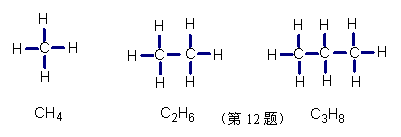
12. 下列是三种化合物的结构式及分子式，如果按其规律，则后一种化合物的分子式应该是
。
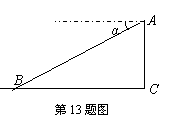
13.如图，某飞机于空中A处探测倒地面目标B，此时从飞机上看目标B的俯角α=30°，飞行高度AC=1200米，则飞机到目标B的距离AB为 。
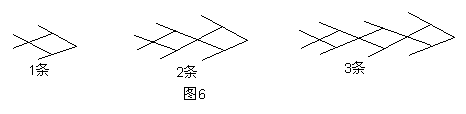
14.如图6是小亮用8根，14根、20根火柴搭的1条、2条、3条“金鱼”，按此方法搭n 条“金鱼”需要火柴__________根。(用含n的代数式表示)
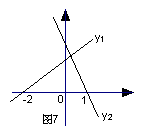
15.如图7是一次函数y1 = ax + b， y2 = kx + c的图象，观察图象，
写出同时满足y1＞0，y2≥0时x的取值范围__________________。
三、解答题(本题共5小题，其中16、17题各9分，18、19、20题各10分，共48分)
16.已知
。当x为何值时，y的值为
；
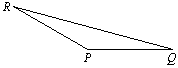
17. 如图：在△RPQ中，已知∠R＝∠Q，请画出△RPQ的外角∠RPM及∠RPM的平分线PO，并证明OP∥RQ．
18. 为了配合“八荣八耻”宣传教育，针对闯红灯的现象时有发生的实际情况，八年级某班开展一次题为“红灯与绿灯”的课题学习活动，它们将全班学生分成8个小组，其中第①～⑥组分别负责早、中、晚三个时段闯红灯违章现象的调查，第⑦小组负责查阅有关红绿灯的交通法规，第⑧小组负责收集有关的交通标志. 数据汇总如下：
| 时间 | 负责组别 | 车流总量 | 每分钟车流量 |
| 早晨上学6：30～7：00 | ①② | 2747 | 92 |
| 中午放学11：20～11：50 | ③④ | 1449 | 48 |
| 下午放学5：00～5：30 | ⑤⑥ | 3669 | 122 |
部分时段车流量情况调查表
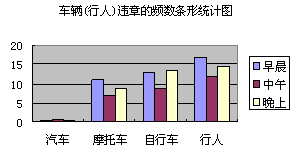
回答下列问题：
⑴请你写出2条交通法规：
① .
② .
⑵画出2枚交通标志并说明标志的含义.
标志含义: 标志含义:
⑶早晨、中午、晚上三个时段每分钟车流量的极差是 ，这三个时段的车流总量的中位数是 .
⑷观察表中的数据及条形统计图，写出你发现的一个现象并分析其产生的原因.
⑸通过分析写一条合理化建议.
19. （10分)阅读下列材料，并解决后面的问题．
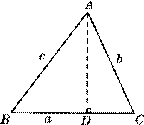在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c．过A作AD⊥BC于D(如图)，则sinB=
，sinC=
，即AD=csinB，AD=bsinC，于是csinB=bsinC，即
．
同理有
，
．
所以
.…………(*)
即：在一个三角形中，各边和它所对角的正弦的比相等．
（1）在锐角三角形中，若已知三个元素a、b、∠A，运用上述结论(*)和有关定理就可以求出其余三个未知元素c、∠B、∠C，请你按照下列步骤填空，完成求解过程：
第一步：由条件a、b、∠A 
∠B；
第二步：由条件 ∠A、∠B ∠C；
第三步：由条件
c．
（2）如图，一货轮在C处测得灯塔A在货轮的北偏西30°的方向上，随后货轮以28.4海里／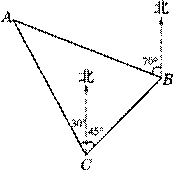
时的速度按北偏东45°的方向航行，半小时后到达B处，此时又测得灯塔A在货轮的北偏西70°的方向上，求此时货轮距灯塔A的距离AB(结果精确到0．1．参考数据：sin40°=0．643，sin65°=0.906，sin70°=0．940，sin75°=0.966)．
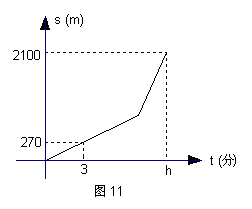
20.小明从家到学校，开始步行，后来跑步，小明离家
的路程S(m)与所用时间t (分)之间的关系如图11所示。
⑴根据图象回答：小明家距学校的路及小明步行的速度。
⑵若h≤8,小明跑步速度为210 m/分，求小明至少需要跑几
分钟。
四、解答题(本题共3小题，其中21题7分，22、23题各8分，共23分)
21. （1）计算：
；
（2）解方程组：
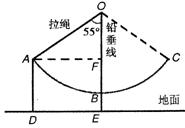22（8分）如图，秋千拉绳OB的长为3米，静止时，踏板到地面的距离BE长时0.6米（踏板的厚度忽略不计），小亮荡该秋千时，当秋千拉绳有OB运动到OA时，拉绳OA与铅垂线OE的夹角为55°，请你计算此时该秋千踏板离地面的高度AD是多少米？（精确到0.1米）
23.如图15，△P1OA1，△P2A1A2，△P3A2A3……△PnAn－1An都是等腰直角三角形，点P1、P2、P3……Pn都在函数
(x > 0)的图象上，斜边OA1、A1A2、A2A3……An－1An都在x轴上。
⑴求A1、A2点的坐标；
⑵猜想An点的坐标(直接写出结果即可)
五、解答题 (本题共3小题，24、25题各12分，26题10分，共34分，
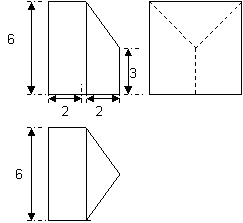24 .据三视图描述物体的形状，试画出物体的表面展开图。并计算该物体的侧面展开图的面积。（图中标有尺寸）
（图中的三角形均是等腰三角形）
25.科幻小说《实验室的故事》中，有这样一个情节：科学家把一种珍奇植物分别放在不同温度的环境中，经过一定时间后，测试出这种植物高度的增长情况（如下表）。
| 温度t / | -8 | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
| 植物高度增长量l/mm | 1 | 24 | 39 | 49 | 49 | 41 | 25 | 1 |
由这些数据，科学家推测出植物高度的增长量l与温度t的函数关系，并由它推测出最合适这种植物生长的温度。
你能想出科学家是怎样推测的吗？若能，请推测出最合适这种植物生长的温度，并写出你的推测探究过程。
26. 设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．
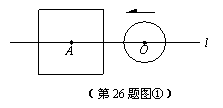
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 | 公共点的个数 |
| d＞a＋r |
|
| d＝a＋r | |
| a－r＜d＜a＋r | |
| d＝a－r | |
| d＜a－r |
所以，当r＜a时，⊙O与正方形的公共点的个数可能有 个；
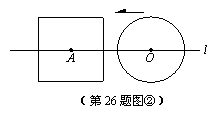
（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 |
|
| d＞a＋r | |
| d＝a＋r | |
| a≤d＜a＋r | |
| d＜a |
公共点的个数所以，当r＝a时，⊙O与正方形的公共点个数可能有 个；
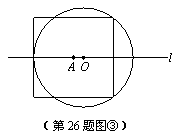（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝
a；
（4）就r＞a的情形，请你仿照“当……时，⊙O与正方形的公共点个数可能有
个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．
（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）