初三数学四月月考题
班级：________姓名:________ _学号:______ _得分:_______
A卷(共100分)
一、选择题：本大题共10个小题，每小题3分，共30分. 在每小题给出的四个选项中，只有一个选项符合题意要求.
1.
的绝对值是（ ）
A.
-2 B.
C.
2 D. 
2. 图1所示的几何体的右视图是（ ）
3. 某服装销售商在进行市场占有率的调查时，他最应该关注的是（ ）
A. 服装型号的平均数 B. 服装型号的众数
C. 服装型号的中位数 D. 最小的服装型号
4. 下列命题中，正确的是（ ）
A. 同位角相等 B. 平行四边形的对角线互相垂直平分
C. 等腰梯形的对角线互相垂直 D. 矩形的对角线互相平分且相等
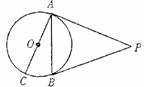5. 如图，已知 PA、PB 是⊙O 的切线，A、B为切点，
AC 是⊙O 的直径，∠P = 40°，则∠ BAC 的大
小是（ ）
A 70° B 40° C 50° D 20°
6. 不等式组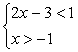
的解集在数轴上可表示为 （ ）
A、
B、
C、
D、
7. 关于x的方程
有两个不相等的实数根，则k的取值范围是 （ ）
A．k＞-1 B．k≥-1 C．k＜1 D．k≥0
8. 已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标
为(-2，-1)，则它的另一个交点的坐标是（ ）
A. (2，1) B. (-2，-1) C. (-2，1) D. (2，-1)
9. 若“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，
4！=4×3×2×1，…，则
的值为（ ）
A. 
B. 99! C. 9900 D. 2！
10. 已知圆锥的侧面展开图的面积是15πcm2，母线长是5cm，则圆锥的底面半径为
（ ）
A．
cm B．3cm C．4cm D． 6cm
二、填空题：本大题共6个小题,每小题3分,共18分.把答案直接填在题中横线上.
11. 若1000张奖券中有200张可以中奖，则从中任抽1张能中奖的概率为______.
12. 若实数m,n满足条件m+n=3，且m-n=1，则m=________，n=___________.
13. 在△ABC中，若D、E分别是边AB、AC上的点，且DE∥BC，AD=1，DB=2，
则△ADE与△ABC的面积比为____________.
14. 函数
的自变量x的取值范围是_______________.
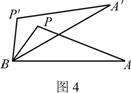
15. 如图4，如果△APB绕点B按逆时针方向旋转30°后得到
△A＇P＇B，且BP=2，那么PP＇的长为____________.
(不取近似值. 以下数据供解题使用：sin15°=
，cos15°=
)
16. 已知n(n≥2)个点P1，P2，P3，…，Pn在同一平面内，且其中没有任何三点在同一直线上. 设Sn表示过这n个点中的任意2个点所作的所有直线的条数，显然，S2=1，S3=3，S4=6，S5=10，…，由此推断，Sn=______________.
三. 解答题：(共52分). 解答应写出必要的文字说明,证明过程或演算步骤.
17. (本题共14分,每小题满分7分)
(1) 计算:
(2) 先化简．再求值：
，其中
；
18. (本小题满分7分)
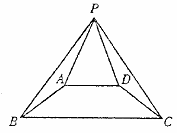
如图，已知四边形ABCD是等腰梯形，AB=DC，AD∥BC，PB = PC.求证：PA=PD.
19. (本小题满分7分)
为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图（如图4），图中从左到右依次为第1、2、3、4、5组。
（1） 求抽取多少名学生参加测试？
（2） 处于哪个次数段的学生数最多？（答出是第几组即可）
（3） 若次数在5次（含5次）以上为达标，
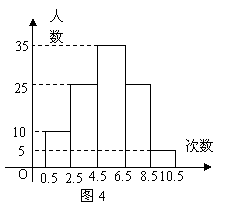求这次测试的达标率。
20. 某影碟出租店开设两种租碟方式：一种是零星租碟，每张收费1元；另一种是会员卡租碟，办卡费每月12元，租碟费每张0.4元 . 小彬经常来该店租碟，若每月租碟数量为x张.
（1）写出零星租碟方式应付金额y1(元)与租碟数量x（张）之间的函数关系式；（2分）
（2）写出会员卡租碟方式应付金额y2(元 )与租碟数量x(张)之间的函数关系式；（2分）
（3）小彬选取哪种租碟方式更合算？（4分）
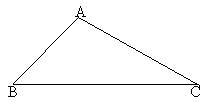21 （7分）如图，点A是一个半径为300米的圆形森林公园的中心，在森林公园附近有B、C两个村庄，现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通.经测得∠ABC=45°，∠ACB =30°，问此公路是否会穿过该森林公园？请通过计算进行说明.
22. (本小题满分9分)
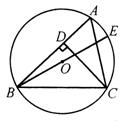
已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高．
（1）求证：AC·BC＝BE·CD ；
（2）已知CD＝6，AD＝3，BD＝8，求⊙O的直径BE的长．
B卷(共20分)
一、填空题（每小题2分，共6分）
1．当a
时，化简
的结果是
。
2．定义：如果ab＝N（a >0, a≠1, N>0）,则b叫做以a为底N的对数，记作b＝logaN.
例如，因为23＝8，所以log28＝3；因为2－3＝，所以log2＝－3.
根据定义计算：①log381＝______；②若logx16＝4,则；x＝________；
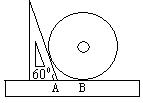3．如图所示，小明同学测量一个光盘的直径，
他只有一把直尺和一块三角板，他将直尺、光盘
和三角板如图所示放置于桌面上，并量出
AB=3.5cm，则此光盘的直径是__________cm。
二、. (本小题满分6分)
已知某项工程由甲、乙两队合做12天可以完成，共需工程费用13800元，乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的2倍少10天，且甲队每天的工程费用比乙队多150元.
(1) 甲、乙两队单独完成这项工程分别需要多少天？
(2) 若工程管理部门决定从这两个队中选一个队单独完成此项工程，从节约资金的角度考虑，应该选择哪个工程队？请说明理由.
三、（8分）已知二次函数
的图象与x轴从左到右两个交点依次为A、B，与y轴交于点C，
（1）求A、B、C三点的坐标； （2）求过B、C两点的一次函数解析式；
（3）如果P(x，y)是线段BC上的动点，O为坐标原点，试求△POA的面积S与x之间的函数关系式，并求出自变量x的取值范围；
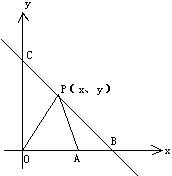（4）是否存在这样的点P，使得PO=AO，若存在，求出点P的坐标；若不存在，说明理由。