梯形

梯形

一、选择题

　1.有两个角相等的梯形是(　 )

　　A.等腰梯形　　　 B.直角梯形;　C.一般梯形　　　 D.直角梯形或等腰梯形

　2.下列命题正确的是(　 )

　　A.凡是梯形对角线都相等;　B.一组对边平行,另一组对边相等的四边形是梯形

　　C.同一底上的两个角相等的梯形是等腰梯形;　D.只有两个角相等的梯形是等腰梯形

　3.在四边形ABCD中,AD∥DC,AC=BD,则四边形ABCD中(　 )

　　A.平行四边形　　　B.等腰梯形;　　C.矩形　　　　　  D.等腰梯形或矩形

　4.下列命题,错误命题的个数是(　 )

　　①若一个梯形是轴对称图形,则此梯形一定是等腰梯形;

②等腰梯形的两腰的延长线与经过两底中点的直线必交于一点;

 ③一组对边相等而另一组对边不相等的四边形是梯形;

④有两个内角是直角的四边形是直角梯形.

　　  A.1个　　 B.2个　　  C.3个　　　D.4个

　5.已知梯形的中位线长为24厘米,上、下底的比为1:3,则梯形的上、 下底之差是(　 )

　　A.24厘米　　 B.12厘米;　　　 C.36厘米　　 D.48厘米

　6.直角梯形的斜腰和下底长都等于a,斜腰和下底的夹角是60°,则梯形的上、 下底之差是(　 )

　　A.a　 B.a　　　C.a　　D.

　7.下列关于等腰梯形的判断,正确的是(　 )

　　A.两底相等;　B.同底上的两底角互补; C.两个角相等; D.对角线交点在对称轴上

　8.已知梯形的两个对角分别是78°和120°,则另两个角分别是(　 )

　　A.78°或120°　　  B.102°或60°;　 C.120°或78°　　  D.60°或120°

　9.等腰梯形的上底下高相等,下底是上底的三倍,则下底角的度数是(　 )

　  A.30°　　　　 B.45°;　　C.45°或135　　D.60°

二、填空题

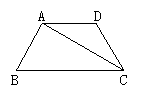
　1.如图所示,在梯形ABCD中,如果AD∥BC.AB=CD,∠B=60°,AC⊥AB,那么∠ACD= _________,∠D=_________.

　　　

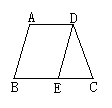
　2.如图所示,在梯形ABCD中,BC∥AD,DE∥AB,DE=DC,∠A=100°,则∠B=_____,∠C=_________,∠ADC=______,∠EDC=________.

　3.等腰梯形的上、下底长分别为6cm,8cm, 且有一个角是60 °, 则它的腰长为_____.

　4.如果等腰梯形的高等于腰长的一半,则它的四个角分别等于_______.

三、解答题

1.你能否找到一个梯形, 使得四个顶点中的任意三个顶点都能连成一个等腰三角形?这是美国大数学家爱尔特希提出的问题中的一部分.在阅读下面的段落前, 你先与同学们探讨一下,图中是一个等腰梯形,其中∠A=72°,AD=DC=CB,AB∥DC. 你能说明,为什么A,B,C,D中任意三点都能构成等腰三角形吗?

 

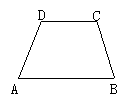
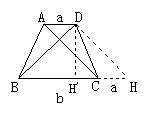
2.如图所示,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD,若两底长分别为a,b,试列出这个梯形的面积S用a,b表示的等式.

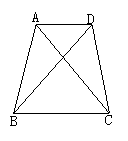
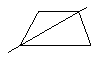
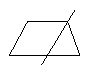
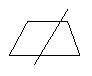
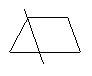
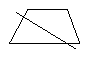
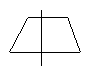
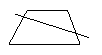
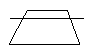
3.用一条直线将一个梯形分割成两部分,则梯形被分成了两个什么样的图形?请尽可能多地画出各种情形.

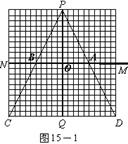
4、（05河北实验）图15―1至15―7中的网格图均是20×20的等距网格图（每个小方格的边长均为1个单位长）。侦察兵王凯在P点观察区域MNCD内的活动情况。当5个单位长的列车（图中的　　 ）以每秒1个单位长的速度在铁路线MN上通过时，列车将阻挡王凯的部分视线，在区域MNCD内形成盲区（不考虑列车的宽度和车厢间的缝隙）。设列车车头运行到M点的时刻为0，列车从M点向N点方向运行的时间为t（秒）。

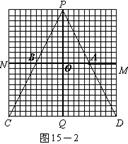
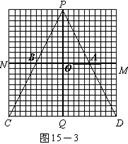
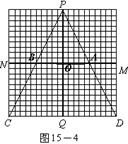
⑴在区域MNCD内，请你针对图15―1，图15―2，图15―3，图15―4中列车位于不同位置的情形分别画出相应的盲区，并在盲区内涂上阴影。

⑵只考虑在区域ABCD内开成的盲区。设在这个区域内的盲区面积是y（平方单位）。

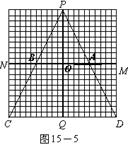
①如图15―5，当5≤t≤10时，请你求出用t表示y的函数关系式；

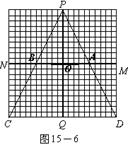
②如图15―6，当10≤t≤15时，请你求出用t表示y的函数关系式；

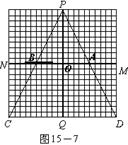
③如图15―7，当15≤t≤20时，请你求出用t表示y的函数关系式；

④根据①~③中得到的结论，请你简单概括y随t的变化而变化的情况。

⑶根据上述研究过程，请你按不同的时段，就列车行驶过程中在区域MNCD内所形成盲区的面积大小的变化情况提出一个综合的猜想（问题⑶是额外加分，加分幅度为1~4分）。

　　 

参考答案:

一、1.D 2.C 3.D 4.B 5.A 6.C 7.D 8.B 9.B

二、1.130° 120° 2.80° 80° 100° 20°　3.2cm　4.30°,150°,150°,30°

三、1.提示:因为四边形ABCD是等腰梯形,

∴∠A=∠B=72°,∠D=∠C=108°,

连结AC,则△ACD是等腰三角形,

连结BD,则△BCD是等腰三角形,△ABD与△ABC都是等腰三角形.

2.提示:如图所示,作DH′⊥BC于H′,DH⊥BD于D,

则,

∵,

∴.

3.如图所示:

4、⑴略；

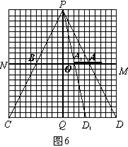⑵①如图6，当5≤t≤10时，盲区是梯形AA₁D₁D

∵O是PQ中点，且OA∥QD，

∴A₁，A分别是PD₁和PD中点

∴A₁A是△PD1D的中位线。

又∵A₁A，∴D₁D

而梯形AA₁D₁D的高OQ=10，

∴

∴

②如图7，当10≤t≤15时，盲区是梯形A₂B₂2C₂2D₂2，

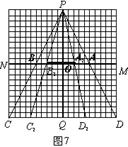易知A₂B₂是△PC₂D₂的中位线，且A₂B₂=5，

∴C₂D₂=10

又∵梯形A₂B₂C₂D₂的高OQ=10，

∴

∴

③如图8，当15≤t≤20时，盲区是梯形B₃BCC₃

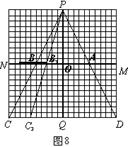易知BB₃是△PCC₃的中位线

且BB₃

又∵梯形B₃BCC₃的高OQ=10，

∴

∴

④当5≤t≤10时，由一次函数的性质可知，盲区的面积由0逐渐增大到75；

当10≤t≤15时，盲区的面积y为定值75；

当15≤t≤20时，由一次函数的性质可知，盲区的面积由75逐渐减小到0

⑶通过上述研究可知，列车从M点向N点方向运行的过程中，在区域MNCD内盲区面积大小的变化是：

①在0≤t≤10时段内，盲区面积从0逐渐增大到75；

②在10≤t≤15时段内，盲区的面积为定值75；

③在15≤t≤20时段内，盲区面积从75逐渐减小到0