第二十四章图形的全等测试题
班级 姓名: 成绩:
一、填空题(每小题3分,共30分)
1、命题“等角的补角相等”,改写成“如果……,那么……”的形式: 。题设是 ,结论是 。
2、如图1, AB=AC,∠1=∠2,AD=AE,则BD= ,∠BAE= 。
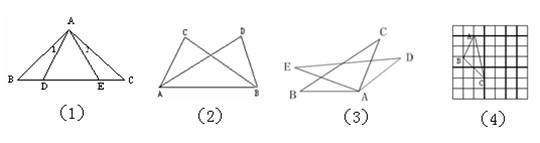
3、如图2,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,至少还需加上条件: 。
4、如图3, △ABC≌△ADE,∠B=35°,∠EAB=21°,∠C=29°,则∠D= ° ,∠DAC= °
5、如图4、在正方形网格上有一个ΔABC,①、作一个与它全等的三角形。②、如每一个小正方形的边长为1,则ΔABC的面积是 。
6、如图5,ΔABC是直角三角形,BC是斜边,将ΔABP绕点A逆时针旋转后,能与ΔABP`重合,如果PA=3,那么PP`= 。
7、已知:如图7,把一张矩形纸片ABCD沿BD对折,使点C落在E处,BE与AD相交于O,写出一组相等的线段 。
8、如图6,已知ΔABC与ΔADE均为等边三角形,且A、B、E三点在同一直线上,请写出图中两对全等三角形 、 。
9、如图8.下面四个条件中,①AE = AD ②AB = AC ③OB = OC ④∠B=∠C
请你以其中两个为已知题设,一个为结论,用“如果……,那么……”的形式,那么写出一个真命题: 。
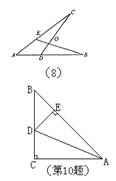
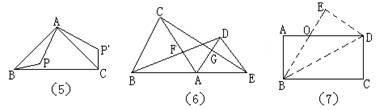
10、如图9,ΔABC,∠C=900,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则ΔDEB的周长为 。
二、选择题(每小题3分,共30分):
1、下列给出的四组条件中,能判定△ABC≌△DEF的是( ).
A.AB=DE,BC=EF, ∠A=∠D; B.∠A=∠D, ∠C=∠F,AC=EF;
 C.∠A=∠D,∠B=∠E,∠C=∠F;
C.∠A=∠D,∠B=∠E,∠C=∠F;
D、AB=DE, BC=EF, △ABC周长=△DEF周长
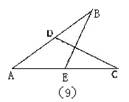
2.如图9,D在AB上,E在AC上,且∠B=∠C,那么补充
下列一个条件后,仍无法判定△ABE≌△ACD的是( ).
A.AD=AE. B.∠AEB=∠ADC.
C.BE=CD. D.AB=AC.
3. 若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( ).
A.5; B.8; C.7; D.5或8.
4. 下列各条件中,不能作出唯一三角形的条件是( )
A. 已知两边和夹角 B. 已知两边和其中一条边所对的角
C. 已知两角和夹边 D. 已知两角和其中一角的对边
5. 求作点P,使P到三角形三边的距离相等的方法是( )
A. 作两边的中垂线的交点 B. 作两边上的高线的交点
C. 作两边上的中线的交点 D. 作两角平分线的交点
6. 命题① 邻补角互补;② 对顶角相等;③ 同旁内角互补;④ 两点之间线段最短;⑤
 直线都相等⑥任何数都有倒数;⑦若
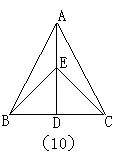
直线都相等⑥任何数都有倒数;⑦若![]() ,则
,则![]() ;⑧ 三角对应相等的两三角形全等 ;⑨ 若∠A+∠B=90°,则∠A与∠B互余
;⑧ 三角对应相等的两三角形全等 ;⑨ 若∠A+∠B=90°,则∠A与∠B互余
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
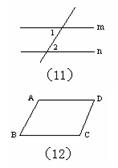
7、如图10,AB=AC,EB=EC,AE的延长线交BC于D,那么图中的全等三角形共有( )对。
A 1对 B 2对 C 3 对 D 4对
 8、下列语句中:① 同角的补角相等;② 雪是白的;③ 画∠AOB=∠1④ 他是小张吗?⑤两直线相交只有一个交点。其中是命题的个数有( )
8、下列语句中:① 同角的补角相等;② 雪是白的;③ 画∠AOB=∠1④ 他是小张吗?⑤两直线相交只有一个交点。其中是命题的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
9、 下列说法正确的是( )
A. 只要有两边对应相等,再有一角对应相等,则这两个三角形全等
B. 如图11,∠1=∠2,则m∥n的理由是“两直线平行,内错角相等”
C. 如图12,若AB=CD,BC=DA,那么∠B=∠D
D. 已知三条线段的长,能画出一个三角形
10、 下列命题中,是假命题的是( )
A. 全等三角形对应边上的高线相等 B. 绝对值等于本身的数是正数
C. 同位角相等,两直线平行 D. 若a=0,则ab=0
三、(每小题4分,共8分)尺规作图:(不写作法,保留作图痕迹)
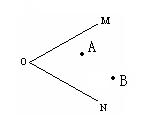
1、 如图,已知∠MON,点A、B,求作:点P,使P到ON和OM的距离相等,且PA=PB。
2、已知:线段a,b求作:ΔABC,使AB=AC,BC=a ,高AD=b
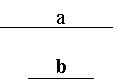
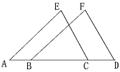
四、(6分)如图.A、B、C、D在同一直线上,EA∥FB, EC∥FD, EC=FD,
求证:AB=CD
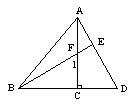 五、(6分)如图,已知AC⊥BD于C,CF=CD,BF的延长线交AD于点E,且AC=BC。求证:(1)
五、(6分)如图,已知AC⊥BD于C,CF=CD,BF的延长线交AD于点E,且AC=BC。求证:(1)![]() ;(2)BE⊥AD。
;(2)BE⊥AD。
六、(6分)等腰三角形底边的中点到两腰的距离会相等吗?若相等,请画出图形,写出已知、求证,并给出证明。若不相等,请说明理由。
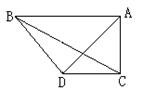
七、(7分)已知,如图AB=2AC,AD=BD,AD平分∠BAC,求证:CD⊥AC,
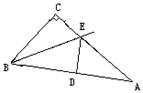
八、(7分)已知△ABC中,∠C = 90°,沿过B的一条直线BE折叠这个三角形,使点C与AB边上的一点D重合。如图所示。要使D恰为AB的中点,还应添加一个什么条件?(请你写出三种不同的添加条件)选择(1)中的某一个添加条件作为题目的补充条件,试说明其能使D为AB中点的理由。
 解:(1)添加条件:①_____________;②_______________;③_____
___。
解:(1)添加条件:①_____________;②_______________;③_____
___。
(2)说明:
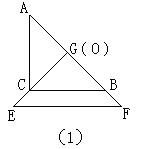
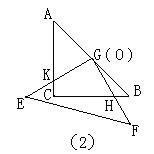
九、(10分)把两个 全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起,如图1,且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,现将三角板EFG绕点O按顺时针方向旋转,四边形CHGK是旋转过程中两三角板的重叠部分(如图所示(2))要上述旋转过程中,BH与CK有怎样的数量关系,四边形CHGK的面积有何变化?证明你发现的结论。