初三年级月考数学试卷
满分：150分
时间：120分钟
一、精心选一选(本大题共12小题，每小题3分，共计36分，注意每小题所给出的四个选项中，只有一项是正确的，请把正确选项前的字母代号填入题前的表格内).
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
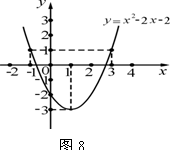
1．如图，已知点A、B、C在⊙O上，∠COA＝100°，则∠CBA的度数是
A.40° B.50° C.80° D.100°
 | |||
 | |||
(第1题) (第5题)
2．函数y=（x＋3）2+1的顶点坐标是
A.（－3,－1） B. (3,1) C. (－3,1) D. (3,－1)
3．已知m是方程x2－x－1＝0的一个根，则代数式m2－m的值等于
A. 1 B.0 C.－1 D.2
4． 与
是同类二次根式的是。
A、
B、
C、
D、
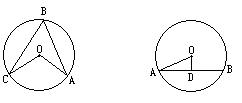
5．如图，AB是⊙O的弦，圆心O到AB的距离OD＝1，若AB＝4，则该圆的半径是
A. B.2 C.
D.3
6．若一个扇形的面积是12π，它的弧长是4π，则它的半径是
A.3 B.4 C.5 D.6
7．若一圆锥的底面半径为2，母线长为4，则其侧面展开图的圆心角是
A.120° B.150° C.180° D.216°
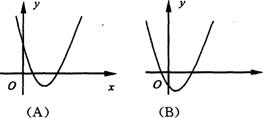
8．已知函数y=x2-2x-2的图象如图8所示，根据其中提供的信息，可求得使y≥1成立的x的取值范围是 （ ）
A．-1≤x≤3 B．-3≤x≤1 C．x≥-3 D．x≤-1或x≥3
9． 二次函数y=2x2+1向下平移3个单位所得函数解析式为
A、y=2x2-2 B、y=2x2+2 C、y=2x2+3 D、y=2x2+4
10．当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是
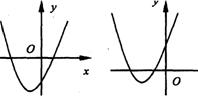
（C） （D）
11.
如右图，一块含有30º角的直角三角形ABC，在水平
桌面上绕点C按顺时针方向旋转到 A’B’C的位置。若BC的长为15cm，那么顶点A从开始到结束所经过的路径长为
A．
cm B．
cm C．
cm D．
cm
12．已知二次函数
，
为常数，当y达到最小值时，x的值为
（A）
（B）
（C）
（D）
二、细心填一填(本大题共6小题，每小题4分，共计24分)
13.已知两圆的圆心距O1O2为3，⊙O1的半径为1，⊙O2的半径为2，
则⊙O1与⊙O2的位置关系为____________________．
14.小明要用一根铁丝制作一个有两条边分别为12cm和25cm的等腰三角形，那么小明所准备的铁丝长度至少应为 ______ cm。
15．两圆有多种位置关系，图中不存在的位置关系是________ （第15题图）
16.二次函数 y=ax2+bx+c与x轴的交点坐标为（3，0）、（-1，0）则一元二次方程ax2+bx+c=0的两根是____________________。
17.已知抛物线y =－2(x+1)2－3，如果y随x的增大而减小，那么x的取值范围是_________
18.如图，在“世界杯”足球比赛中，甲带球向对方球门PQ进攻。当他带球冲到A点时，同伴乙已经助攻冲到B点。有两种射门方式：第一种是甲直接射门；第二种是甲将球传给乙，由乙射门。仅从射门角度考虑，应选择
种射门方式。
三、认真算一算、答一答(本大题共8小题，共计90分).
19．(本题满分8分)
已知
是二次函数，且函数图象有最高点。
（1）求k的值；（2）求顶点坐标和对称轴．
20、(本题满分10分)
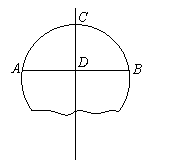
如图，破残的圆形轮片上，弦AB的垂直平分线交AB于C，交弦AB于D.
(1)求作此残片所在的圆(不写作法，保留作图痕迹)；
(2)若AB＝24cm，CD＝8cm，求(1)中所作圆的半径.
 |
21、(本题满分10分)
△ABC 外切于⊙O ，切点分别为点D、E、F，∠A＝600，BC＝7,⊙O的半径为．
⑴求BF+CE的值 ⑵求△ABC的周长．
22．(本题满分12分)将进货单价为40元的商品按50元售出时，就能卖出500个，已知这种商品每个涨价1元，其销售量就减少10个。
（1）问：为了赚得8000元的利润，售价应定为多少？这时进货至少多少个？
（2）当定价为多少元时，可获得最大利润？
23. (本题满分12分)
如图，阴影部分是由4段以正方形边长的一半为半径的圆弧围成的，这个图形被称作为斯坦因豪斯图形．
（1）请你在右边已作好的正方形中作出这四段弧，将其补成斯坦因豪斯图形（不要求写作法，留下作图痕迹，阴影部分用斜线填涂）．
（2）若图中正方形的边长为10，请你求出所作图中阴影部分的面积．
24. (本题满分12分)
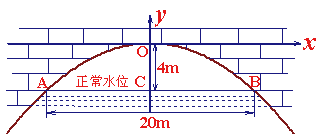
有一座抛物线形拱桥，正常水位时桥下水面宽度为20m，拱顶距离水面4m.
⑴ 在如图所示的直角坐标系中，求出该抛物线的解析式；
⑵ 设正常水位时桥下的水深为2m，为保证过往船只顺利航行，桥下水面的宽度不得小于18m，求水深超过多少米时就会影响过往船只在桥下的顺利航行.
25．(本题满分12分)
东方专卖店专销某种品牌的计算器，进价l2元／只，售价20元／只．为了促销,专卖店决定凡是买10只以上的，每多买一只，售价就降低O.10元(例如．某人买20只计算器，于是每只降价O.10×(20-10)=1元,就可以按19元／只的价格购买)，但是最低价为16元／只．
(1)求顾客一次至少买多少只，才能以最低价购买?
（2）一位顾客一次购买了若干只计算器，专卖店共获利润180元，请你求该顾客所购买的计算器的数量。
（3）有一天，一位顾客买了46只，另一位顾客买了50只，专实店发现卖了50只反而比卖46只赚的钱少，为了使每次卖的多，赚钱也多,在其他促销条件不变的情况下,最低价16元／只至少要提高到多少?
| X只 | … | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | … |
| 利润（元） | 。。。 | 200 | 200.9 | 201.6 | 202.1 | 202.4 | 202.5 | 202.4 | 202.1 | 201.6 | 200.9 | 200 |
以下是小丽在探索该问题时所列的计算器数量与利润关系表格的一部分，此表供你探索问题时参考。。。。。。
26
(本题满分14分)
已知：在四边形ABCD中，AB＝1，E、F、G、H分别时AB、BC、CD、DA上的点，且AE＝BF＝CG＝DH。设四边形EFGH的面积为S，AE＝x(0≤x≤1)。
(1)如图①，当四边形ABCD为正方形时，
<1>求S关于x的函数解析式，并求S的最小值S0；
<2>在图②中画出<1>中函数的草图，并估计S＝0.6时x的近似值(精确到0.01)；
(2)如图③，当四边形ABCD为菱形，且∠A＝30°时，四边形EFGH的面积是否存在最小值？若存在，求出最小值；若不存在，请说明理由。
 |
 |