九年级数学第一次中考模拟考试试卷
数 学
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 总 分 |
| 得分 |
第Ⅰ卷
一、选择题（每小题2分，共24分）
1、如果2
的值等于－2，则的值为（ ）
A．1
B．－1 C．0 D．
２、数轴上的两点A、B分别表示2，－3，则点A、B间的距离为（ ）
A．－1 B．1 C．－5 D．5
3、下列运算正确的是（ ）
A．
B．
C．
D．
4、据统计，到2000年底，我国人口总数已达12．95亿，这个数据用科学记数法可记
为（ ）
A．1．295×10
B．1．295×10
C．12．95×10 D．12．95×10
5、如果x的算术平方根为5，则x的值为（ ）
A．5 B. ±5 C.25 D．±25
6、随机抛掷一枚均匀的硬币两次，有且只有一次正面朝上的概率为（ ）
A. 
B. 
C. 
D．
7、在下列四个图案中，既是轴对称图形，又是中心对称图形的是( )
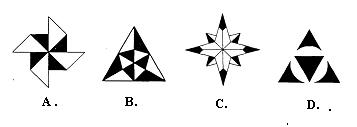
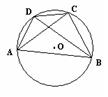8、如图,点A、B、C、D都在⊙O上，点D是弧
的中点，则图中与
∠ABD相等的角共有（ ）
A．1个 B．2个 C．3个 D．4个
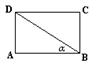
9、如图，矩形ABCD中，AB= 4，AD=3，则cos
的值为（ ）
A．
B. 
C.
D． 
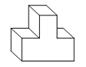
10、一个如图所示的物体放在水平的桌面上，则它的左视图是（ ）
A．
B.
C.
D． 
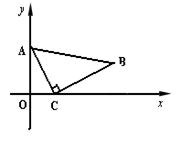
11、△ABC中，∠ACB=90°，将△ABC按如图的位置放在直角坐标系中，若点A的坐标为（0，2），点C的坐标为（1，0），点B的横坐标为4，则点B的纵坐标为( )
A．1 B．1．2 C．1．5 D．1．8
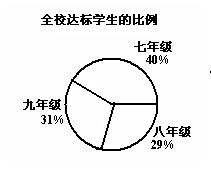
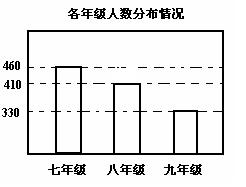
12、某校对全体学生进行体育达标检测，七、八、九三个年级共有900名学生达标，达标情况如下表所示．则下列三位学生的说法中正确的是（ ）
甲：“七年级的达标率最低”；
乙：“八年级的达标人数最少”；
丙：“九年级的达标率最高”
A．甲和乙 B． 乙和丙 C． 甲和丙 D． 甲乙丙
第Ⅱ卷
二、填空题（每小题3分，共12分）
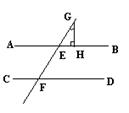
13、如图，已知，AB∥CD，直线EF分别交AB，CD于E、F，点G在直线EF上，GH⊥AB，若∠EGH=32°，则∠DFE的度数为 .
14、已知反比例函数
的图象在每一个象限内 ，
随
的增大而减小 ，那么
的取值范围是_____________.
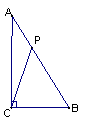
15、如图，△ABC中，∠ACB=90°，∠A=30°，AB=2
㎝，点P从点A出发，沿斜边AB以1㎝/s的速度向点B运动．当△PAC为等腰三角形时，点P的运动时间为
s．
16．如图，在两个同心圆中，大圆中长为16cm的弦AB与小圆相切，则图中圆环的面积为 ．
三、（每小题6分，共24分）
17．计算：
．
18. 解不等式组: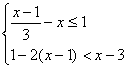 
，并把其解集在数轴上表示出来.
19．如图，在等腰梯形ABCD中，AD∥BC，AB=DC，DE∥AB，AD+DC=BC．
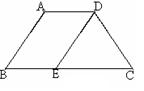求证：（1）DE=DC；
（2）△DEC是等边三角形.
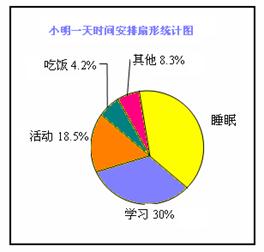20．小明某一天时间安排的统计图如右：
|
|
四、（每小题6分，共12分）
21． 甲、乙、丙三人中，有两人血型为O型，一人血型为A型．在2006年的两次无偿献血活动中，三人中均有一人参加了献血活动．求这两次献血的血型均为O型的概率．（要求：用列表法或画树状图法进行分析、求解）
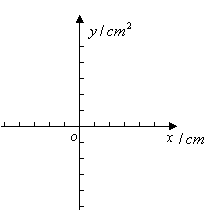22．制作一个底面是正方形的长方体，要求它的体积为
，设底面面积为
，高为
．
（1）试写出与的函数关系式；
（2）在所给坐标系中画出该函数的图象；
（3）当底面正方形边长为
时，求长方体的高．
五、（23题7分，24题8分，共15分）
23. 某校篮球队参加全市中学生篮球比赛，一共比赛16场，得28分.按赛制规定每胜一场得2分，负一场得1分，该校篮球队胜、负各多少场？
24．中国电信2007年开展了“首付198元电信宽带、惠普电脑抱回家”活动，其收费标准如下：
| 分期付款 | 首 付 | 198（元） |
| 月 付（27个月） | 198（元） | |
| 一次付清（免费27个月上网） | 5346（元） | |
其中，宽带业务竣工当月宽带使用费0．5元/小时，超过200元按200元收费。
(1)请根据以上信息分析，在使用时间不少于协议要求的28个月的前提下，选择哪一种方式付款合算？
（2）请写出宽带业务竣工当月宽带使用费（元）和上网时间（小时）之间的函数关系式，并写出自变量取值范围；
（3）如果一个用户3月份办理此业务，当月上网160小时，此后每月仅交费198元，请问到7月份结束时他总共支付给中国电信的费用是多少？
六、（每小题8分，共16分）
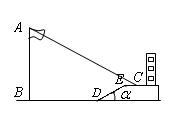25．某中学九年级数学课外学习小组在某天下午进行实践活动时，测量教学楼前的旗杆
的高度，当时阳光从正西方向照射过来（如图），旗杆的顶端
的影子落在教学楼前的平地上
处，斜坡DE与地面的夹角
．测得影长CE=2m，BD=20m，DE=4m．在同一时刻，测得一根长为1 m的直立竹竿的影长为4m．请你根据这些数据求出旗杆的高度．（参考数据：
，要求结果保留两个有效数字）
26．南京某校一个年级的学生进行社会实践活动，两名同学的对话如下：
 |
已知该校共支出门票费1200元，请问该校一共有多少名同学参加了本次社会实践活动？
七、（本题8分）
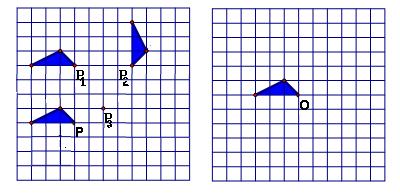
27．（１）如图甲，在方格纸中如何通过平移或旋转这两种变换，由△得到图形B，再由图形B得到图形C（对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回答出旋转中心、旋转方向和旋转角度）；
（２）如图，如果点P、P3的坐标分别为（0，0）、（2，1），写出点P2的坐标；
（３）图7是某设计师设计图案的一部分，请你运用旋转变换的方法，在方格纸中将图形绕点O顺时针依次旋转90°、180°、270°，依次画出旋转后所得到的图形．
注：方格纸中的小正方形的边长为1个单位长度.
八、（本题9分）
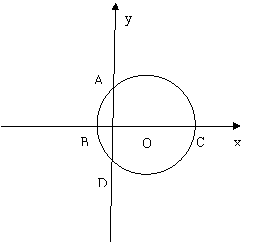
28．如图，⊙O的圆心在轴上，与坐标轴交于A（0，2）、B（
，0），
若抛物线
经过A、B两点，抛物线的顶点为P．
（1） 求出抛物线的关系式；
（2） 抛物线的顶点P是否在圆上？
（3） 若⊙O与轴的另一交点为D，则由线段PA、线段PD及弧ABD形成的封闭图形
PABD的面积为多少？
 |