九年级数学第一学期期末模拟试卷2
一、选择题（30分）
1、下列等式正确的有（ ）
（A）
（B）
（C）
（D）
2、方程
是关于x的一元二次方程，则
满足的条件是（ ）
（A）m≠1 （B）m≠0 （C）m≠1 （D）m＝±1
3、半径为4cm，120°的圆心角所对的弦长为（ ）
(A)5cm；
(B)
cm；
(C)6cm； (D)
cm；
4、下列命题中，假命题是( )
(A)长度相等的弧是等弧； (B)等弧必须是同圆或等圆中的弧，否则不能互相重合；
(C)度数相等的弧不一定是等弧； (D)等弧的度数相等；
5、下列方程中有两个相等的实数根的方程是（ ）
A. 
B. 
C. 
D. 
6、在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中，54.5……57.5这一组的频率是O.12，那么，估计总体数据落在54.5……57.5之间的约有（ ）
A．6个 B．12个 C．60个 D．120．个
7、若△ABC≌△DEF，且△ABC的周长为20，AB＝5，BC＝8,则DF长为（ ）
Ａ．５； Ｂ．８； Ｃ．７； Ｃ．５或８．
8、某学校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？若设原价每瓶
元，则可列出方程为 （ ）
（A）
（B）
（C）
（D）
9、若0<a<1，则点M(a-1，a)在第( )象限（ ）
A．第一 B．第二 C．第三 D．第四
10、已知关于x的方程
的两根的平方和是8，则k的值是（ ）
A. 1 B. 
C. 
D. 
二、填空题（18分）
11、方程
的解是
。
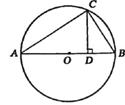
12、如图，AB为⊙O的直径，弦AC=4cm，BC=3cm，CD⊥AB，垂足为D，那么CD的长为____cm．
（1） （2） （3）
13、从一副扑克牌中随机抽出一张牌，得到大王或小王的概率是__________
。
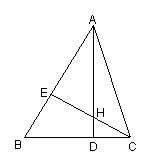
14、如图，点D在AB上，点E在AC上，CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°，则∠C= 。
15、若分式
的值为负数，试确定x的取值范围
。
16、如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD， CE交于点H，请你添加一个适当的条件：____________，使△AEH≌△CEB。
三、解答题（102分）
17、（12分）
已知：
的值。
18、（10分）
在平面直角坐标系中，圆心O的坐标为（-3，4），以半径r在坐标平面内作圆，
（1）当r 时，圆O与坐标轴有1个交点；
（2）当r 时，圆O与坐标轴有2个交点；
（3）当r 时，圆O与坐标轴有3个交点；
（4）当r 时，圆O与坐标轴有4个交点；
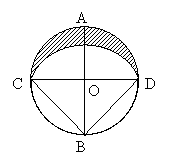
19、如图，已知⊙O的半径为R，直径AB⊥CD。以B为圆心，以BC为半径作弧CED，求弧CED与弧CAD围成的新月形ACED的面积S.
20、有一面积为150m2的长方形鸡场，鸡场的一边靠墙，（墙长18米），另三边用竹篱笆围成，如果竹篱笆的长为35米，求鸡场的长与宽各为多少米？
21、如图，CD⊥AB,BE⊥AC，垂足分别为D、E，BE,CD相交于点O，且∠1=∠2，
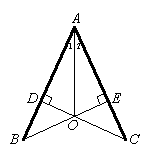试说明OB=OC。
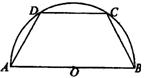22、如图，四边形ABCD内接于半圆O，AB是直径．
（1）请你添加一个条件，使图中的四边形ABCD成等腰梯形，这个条件 是
（只需填一个条件）。
（2）如果CD＝
AB，请你设计一种方案，使等腰梯形ABCD分成面积相等的三部分，并给予证明。
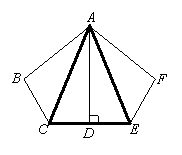
23、已知：如图，AB=AF，BC=FE,∠B=∠F,D是CE的中点。
⑴求证：AD⊥CE;⑵连结BF后，还能得出什么新的结论（请写出两个，不要求证明）？
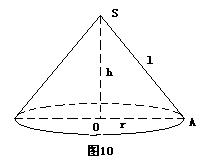24、已知圆锥的底面半径为r＝20cm，高h=
cm,现在有一只蚂蚁从底边上一点A出发。在侧面上爬行一周又回到A点，求蚂蚁爬行的最短距离。
答案
一、选择题（30分）
1、下列等式正确的有
（A） （B） （C） （D）
2、方程是关于x的一元二次方程，则满足的条件是 （ ）
（A） m≠1 （B） m≠0 （C） m≠1 （D） m＝±1
3、半径为4cm，120°的圆心角所对的弦长为
(A)5cm；(B)cm；(C)6cm；(D)cm；
4、下列命题中，假命题是( )
(A)长度相等的弧是等弧； (B)等弧必须是同圆或等圆中的弧，否则不能互相重合；
(C)度数相等的弧不一定是等弧； (D)等弧的度数相等；
5、下列方程中有两个相等的实数根的方程是（ ）
A. B.
C. D.
6、在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中，54.5……57.5这一组的频率是O.12，那么，估计总体数据落在54.5……57.5之间的约有
A．6个 B．12个 C．60个 D．120．个
7、若△ABC≌△DEF，且△ABC的周长为20，AB＝5，BC＝8,则DF长为（ ）.
Ａ．５； Ｂ．８； Ｃ．７； Ｃ．５或８．
8、某学校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？若设原价每瓶元，则可列出方程为
（A）
（B）
（C）
（D）
9、若0<a<1，则点M(a-1，a)在第( )象限
A．第一 B．第二 C．第三 D．第四
10、已知关于x的方程的两根的平方和是8，则k的值是（ ）
A. 1 B.
C. D.
二、填空题（18分）
11、方程的解是 
12、如图，AB为⊙O的直径，弦AC=4cm，BC=3cm，CD⊥AB，垂足为D，那么CD的长为____cm．
（1） （2） （3）
13、从一副扑克牌中随机抽出一张牌，得到大王或小王的概率是__________。
14、如图，点D在AB上，点E在AC上，CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°，则∠C= 20°
15、若分式的值为负数，试确定x的取值范
围 x＜－1或x＞2
16、如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD， CE交于点H，请你添加一个适当的条件：____________，使△AEH≌△CEB。AH=CB等
三、解答题（102分）
17、（12分）
已知：的值。
18、（10分）
在平面直角坐标系中，圆心O的坐标为（-3，4），以半径r在坐标平面内作圆，
（1）当r 时，圆O与坐标轴有1个交点；
（2）当r 时，圆O与坐标轴有2个交点；
（3）当r 时，圆O与坐标轴有3个交点；
（4）当r 时，圆O与坐标轴有4个交点；
（1）r=3；（2）3＜r＜4；（3）r=4或5；（4）r＞4且r≠5；
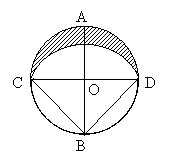19、如图，已知⊙O的半径为R，直径AB⊥CD。以B为圆心，以BC为半径作弧CED，求弧CED与弧CAD围成的新月形ACED的面积S.
20、有一面积为150m2的长方形鸡场，鸡场的一边靠墙，（墙长18米），另三边用竹篱笆围成，如果竹篱笆的长为35米，求鸡场的长与宽各为多少米？
长为15米，宽为10米
21、如图，CD⊥AB,BE⊥AC，垂足分别为D、E，BE,CD相交于点O，且∠1=∠2，试说明OB=OC.
因为CD⊥AB,BE⊥AC，
所以∠ADO=∠AEO=90°
又因为∠1=∠2，AO＝AO，
所以△ADO≌△AEO (AAS)
所以 DO=OE
又因为∠BDO=∠CEO＝90°，∠BOD=∠EOC，
所以 △BDO≌△CEO （ASA）
所以 OB=OC.
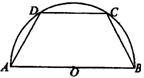22、如图，四边形ABCD内接于半圆O，AB是直径．
（1）请你添加一个条件，使图中的四边形ABCD成等腰梯形，这个条件 是
（只需填一个条件）。
（2）如果CD＝AB，请你设计一种方案，使等腰梯形ABCD分成面积相等的三部分，并给予证明。
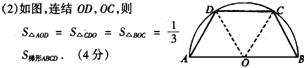
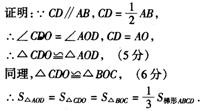
23、.已知：如图，AB=AF，BC=FE,∠B=∠F,D是CE的中点。
⑴求证：AD⊥CE;⑵连结BF后，还能得出什么新的结论（请写出两个，不要求证明）？
⑴连结AC、AE,可先证△ABC≌△AFE; ⑵如果AD⊥BF,AD平分BF,BF∥CE等。
24、已知圆锥的底面半径为r＝20cm，高h=cm,现在有一只蚂蚁从底边上一点A出发。在侧面上爬行一周又回到A点，求蚂蚁爬行的最短距离。
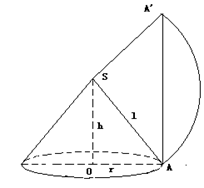
80
cm；提示：由r=20cm，h=20
cm，可得母线l=80cm，而圆锥侧面展开后的扇形的弧长为
，可求得圆锥侧面展开后的扇形的圆心角为900，故最短距离为80cm。