九年级数学第一学期期未测验题

九年级数学第一学期期未测验题

（满分150分，时间120分钟）

　　　　　　　　　　

题　号	一	二	三	四	总　分
得　分

一．选择题：（每小题4分，共48分 ）在每个小题的下面，都给出了代号为A、B、C、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在题后的括号中．

1、下列各式中，运算正确的是（　　）

A. a²·a³=a⁶　　　　　　　　　　B. ()^-2+200⁰=4

C. (-)²= 　　　 　　　　　D. -21a²b³c÷3a²b=-7b²

2、计算的结果是(　　 )

A.　　　  B.　　  C.　　  　 D.

3、关于的一元二次方程的一个根是0，则的值为（　　　）

A.- 1　　 　　　 B.1　　　　 　 C.1或　　 　 D.0.5

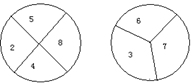
4、如图，两个标有数字的轮子可以分别绕轮子中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数

字，这两个数字和为奇数的概率是（　　 ）

A.　　　B. 　 C. 　 D.

5、下列说法正确的是（　　 ）

A. 三点确定一个圆。　　　　　　 　　　

B. 三角形的内心到三角形三个顶点距离相等。

C.和半径垂直的直线是圆的切线。 　　　

D.一个三角形只有一个外接圆。

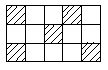
6、一只小狗在如图的方砖上走来走去，最终停在阴影方砖上的概率是（　  ）

A. 　　　　　B. 　　 　　　 C. 　　D.

7、要使分式（－ ）÷的值是负整数，则a应取的数为（　　）

A. 1和2　　　　　　 B. 2和3　　　　　　 C. a＞1　　　　　　　 D. a＞2

8、若圆锥的母线长为4cm，底面半径为3cm，则圆锥的侧面展开图的面积是（　　　）

A. ；　　B. ；　　C. ；　　 D. ；

9、一个直角三角形斜边长为，内切圆半径为，则这个三角形周长是（　 ）

A.　 　　 B.　　　　 C.　　 　　　D.

10、下列说法错误的是（　　 ）

A. 顶角和腰对应相等的两个等腰三角形全等

B. 顶角和底边对应相等的两个等腰三角形全等

C. 斜边对应相等的两个等腰直角三角形全等

D. 两个等边三角形全等

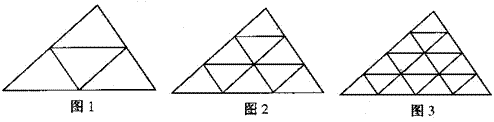11、如图，将一个三角形的三边依次都分成2、3、4……等分，并将分点按图1、图2、图3那样连起来，这样，每个图中所得到的小三角形都会全等．按此方法，当三边都分成10等分时，所得到的全等小三角形的个数是(　　)．

A . 98　　　　　　　 B . 99　　 　　　　　　　C . 100　 　　　　　D. 101

12、有一个边长为6㎝的正三角形ABC木块，点P是边CA的延长线上的点，在A、P之间拉一条细绳，绳长AP为15㎝，握住点P，拉直细绳，把它全部紧紧缠绕在△ABC木块上（缠绕时木块不动）。若圆周率取3.14，则点P运动的路线长为（精确到0.1㎝）（　　）

　　A. 28.3㎝　　　　　 B. 28.2㎝　　　　　 C. 56.5㎝　　　　 D. 56.6㎝　

二、填空题（每小题4分，满分40分）请将答案直接填在题后的横线上。

13、氧原子的直径约为0.m，用科学记数法表示为　　　　 。

14、当m= 　　　　 时，方程是一元二次方程。

15、已知分式，当x=2时，分式无意义；当x=4时，分式的值为零，则b^a=　　　 。

16、方程x²+5x-m=0的一个根是2，则m=　　；另一个根是　　 。

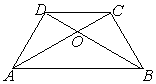
17、等腰梯形ABCD中，AB∥CD,

对角线AC与BD相交与O,请写出图中

一对相等的线段　　　　　 。

18、正方形ABCD的边长是2cm,以直线AB为轴旋转一周，所得到的圆柱的侧面积为 　　　　　 cm².　　　　　　　　　　　　　 

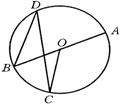
19、如图、AB是⊙O的直径，弦CD⊥AB,垂足为P，如AP∶PB=1∶4,CD=8,则AB= 　　  .

　　C　　　　　　　 

A　　　　　  B

D 

(19题)　　　　　　　 (20题)　　　　　　　 (21题)

20、如图，在⊙O中，AB是⊙O的直径，∠D＝40°，则∠AOC的度数为___　　 .　　

21、如图,已知AC=BD,则再添加条件　　　　  ,可证出:△ABC≌△BAD.

22、为了测量一个圆形铁环的半径，小华采用了如下方法：将铁环平放在水平桌面上，用一个锐角为30°的直角三角板和一个刻度尺，按如图所示的方法得到有关数据，进而求得铁环的半径，若测得AB=10㎝，则铁环的半径是　　　　  。

三、解答题：（每小题8分，共32分）下列各题解答时必须给出必要的演算过程和推理步骤

23、计算:  

24、解方程：）　　

25、化简：

26、九年级6班有48名同学，其中男生30人．在一节数学课上，老师叫班上每个同学把自己的名字(没有同名)各写在一张大小、形状都相同的小卡片上，并放入一个盒子里摇匀．

(1) 如果老师随便从盒子中取出一张小卡片，则每个同学被抽到的概率是多少?

(2) 如果老师随便从盒子中抽出一张小卡片，那么抽到男同学的概率大还是抽到女同学的概率大?

　  (3) 若老师已从盒子中抽出了10张小卡片，其中有4个是男同学，并把这10张小卡片放在一边，再从盒子中抽出第11张小卡片，则这时女同学被抽到的概率是多少?

四、解答题：（每小题10分，共30分）下列各题解答时必须给出必要的演算过程和推理步骤

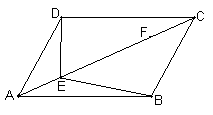27、如图，在平行四边形ABCD中，点E、F在对角线AC上，且AE=CF，请你以F为一个端点和图中已表明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）。

（1）连结　　　　 ；

（2）猜想：　　  = 　　；

（3）证明：

28、今年五月，某工程队（有甲、乙两组）承包人民路中段的路基改造工程，规定若干天内完成．

（1）已知甲组单独完成这项工程所需时间比规定时间的2倍多4天，乙组单独完成这项工程所需时间比规定时间的2倍少16天．如果甲、乙两组合做24天完成，那么甲、乙两组合做能否在规定时间内完成？

（2）在实际工作中，甲、乙两组合做完成这项工程的后，工程队又承包了东段的改造工程，需抽调一组过去，从按时完成中段任务考虑，你认为抽调哪一组最好？请说明理由．

29、如图，AB、AC分别是⊙O的直径和弦，D是劣弧AC的中点，DE⊥AB于H，交⊙O于点E，交AC于点F．

（1）图中有哪些必相等的线段？（要求：不要标注其它字母，找结论的过程中所作的辅助线不能出现在结论中，不必写出推理过程．）

（2）若过C点作⊙O的切线PC交ED延长线于P点，（请补全图形），

求证：PF²=PD·PE；

（3）已知AH＝1，BH＝4，求PC的长．　　　　　  　　　　 

　　 C

　　　　　　　　　　　　　　　　　　　　　　  　

　　　　　　　　　　　　　　　　　　　　　　  F

　　　　　　　　　　　　　　　　　　　　　 　　 H  　　O  　

　　　　　　　　　　  　　　　　　　　　　　 

九年级数学第一学期期未测验题

参考答案

一、选择题：

1.C,2.D,3.A,4.B,5.D,6.B,7.B,8.B,9.B,10.D,11.C,12.C

二、填空题：

13. 1.6×10^-9 ； 14. m=3 ；15. 1/16 ；16. 14，-7；17. AC=BD等；

18. 8；19. 8；20. 100°； 21. ∠CAB=∠DBA等；22. 10　.

三、解答题：

　　　 23. 5

　　　 24. 3x²+x-2=0　x₁= -1,x₂=

　　　 25. 2x-4

　 26. （1）1/48；（2）抽到男同学的概率大；（3）6/19

四、解答题：

27. 略

　　 28. 解：（1）设规定时间为x天，则

　　　  　　 解之，得x=28，x=2

　　经检验可知x=28，x=2都是所列方程的根，但x=2不合题意，舍去，

只取x=28

由24＜28知，甲、乙两组合做可在规定时间内完成．

（2）设甲、乙两组合做完成这项工程的用去了y天，则

　解之，得y=20（天）

甲独做剩下工程所需的时间：（天）

∵20+10=30＞28，∴甲独做剩下的工程不能在规定时间内完成；

乙独做剩下工程所需的时间：（天）

∵20+6=26＜28，∴乙独做剩下的工程能在规定时间内完成．

∴我认为抽甲组最好．

　29. 解答（1）AO＝BO，DH＝EH，DF＝AF，AC＝DE……4分

（2）证明：连EC，AE，

　　　　　则∠PFC是ΔECF的一个外角，于是∠PFC＝∠ACE＋∠FEC

∵DH⊥AB，AB是⊙O的直径，

　　　　  ∴A是DE中点，即AD=AE，　　　　　　　　 P

　  C

　　　　  ∴∠AED＝∠ACE　……5分　　　　　　　 D　　

　　　　∴∠ACE＋∠FEC＝∠AED＋∠DEC＝∠AEC．　　　　　　　　 

　　　　　　　　　　　　 ………………6分　　A 　　 F　　　　　 B

　　　　∵PC是⊙O的切线，　　　　　　　　　　　  H　　O 　　　

　　 　　 ∴∠PCA＝∠AEC．

　　　　　∴∠PCA＝∠PFC，　　　　　　　　　　　 E

　　　　　∴PC＝PF．……………7分　　　　　　　　　　　　

　　　　  ∵PC是切线　　　　　　　　　　　　　　　　　　　

∴，∴．……8分

（3）在⊙O中，AHHB＝DHHE＝DH，

∴　

设AF＝，则．

在中，

∴，∴，即．　

于是．……10分

由（1）（2）知，

，解得．∴＝．

　∴PC=PF=…12分