九年级数学第一学期期中考试试卷  

亲爱的同学，这份试卷将再次记录你的自信、沉着、智慧和收获. 教师一直投给你信任的目光.请认真审题，看清要求，仔细答题，祝你考出好成绩。

一. 仔细选一选 (本题有15个小题, 每小题3分, 共45分)

　　下面每小题给出的四个选项中, 只有一个是正确的, 请把正确选项前的字母填在

答题卷中相应的格子内.

1. 在实数3.14，，π，0.，0,，中，无理数的个数为(　　　)

A．2个　　　　 B．3个　　　　　 C．4个　　　　　 D．5个

2、用四舍五入得到的近似数中，含有三个有效数字的是（　 ）

A、0.5180　　  B、0.05180　　　 C、800万　　　　  D、5.0018

3、观察下面图案，在A、B、C、D四幅图案中，能通过图案(1)的平移得到的是..(　　　)

　

4、某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案，你认为符合条件的是（　　  ）

A　正三角形　　　　  B　正五边形　　 C　等腰梯形　　　  D　 菱形

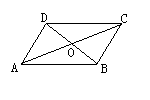5.  如图，ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取什范围是（　　）

A．1＜m＜11　　　　　　 B．2＜m＜22　　　　 

C．10＜m＜12　　　　　  D．5＜m＜6

y

y

y

y

6、面积为2的△ABC，一边长为x,这边上的高为y,则y与x的变化规律用图像表示大致是（　　  ）

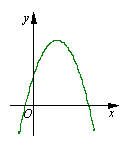
7、二次函数y＝ax²＋bx＋c的图像如图所示，则关于此二次函数的

下列四个结论①a<0　 ②a>0　 ③>0　④<0中，正确的结论有　　（　　 ）

A.1个　　　　 B.2个　　　　  C.3个　　　　　　 D.4个

　　　　　　　　　　　

8.盒子中装有1个白球和2个红球，从中摸出一个球，放回搅匀后再摸出第二个球，则下列事件中，机会最小的事件是(　　  )

A．两个红球　　　B．两个白球　　 C．一红一白　　　D．无法确定

9、对于函数y＝-x²＋2x-2，使得y随x的增大而增大的x的取值范围是（　　）

A．x﹥－１　B．x≥１　　C．x≤１　　　D．x﹤－１

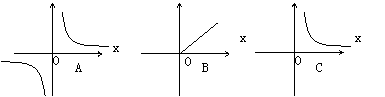
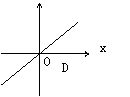
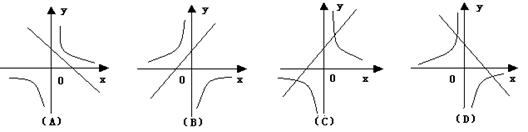
10、在同一直角坐标系中，函数y=kx+k，与y=k/x的图像大致为　　　 （　　）

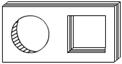
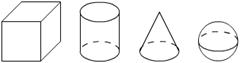
11、如左下图是一块带有圆形空洞和方形空洞的小木板，则有下列物体各若干，既可以堵住圆形空洞，又可以堵住方形空洞的是  （　　 ）　　　　　　　　　　　　　　　　　　　　　　　　　　

 

　　 A　　　  B　　　 C　　　D

12、有如下结论（1）有两边及一角对应相等的两个三角形全等；（2）菱形既是轴对称图形又是中心对称图形； （3）对角线相等的四边形是矩形； （4）平分弦的直径垂直于弦，并且平分弦所对的两条弧,　 （4）如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形；（5）半径为5的圆中，弦AB=8，则圆周上到直线AB的距离为2的点共有3个；

其中,正确结论的个数为（　 ）

A、1个　　　　B、2个　　　　 C、3个　　　　　  D、4个

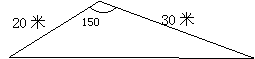
13、某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要　　　　　　 （　　）

　　　A．450a元　　　

 B．225a元　　

 C．150a元　

 D．300a元

14、点P为⊙O内一点，且OP＝4，若⊙O的半径为6，则过点P的弦长不可能为　（　 ）

A 　　　B　12　　　　 C　8　　　  D　10.5

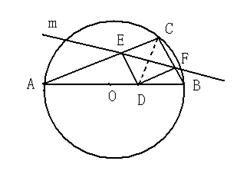
15、九年级的玲玲从小就喜欢画画，请看她的研究：

（1）　  以AB为直径画半⊙O；

（2）　  在半⊙O上任意取一点C；

（3）　  画∠ACB的平分线与AB相交于D；

（4）　  画CD的中垂线m与AC、BC分别相交于E、F；

（5）　  连接DE、DF。

她发现结论：（a）∠ADE于∠BDF互余；（b）四边形CEDF为正方形；

（c）把△BFD绕着D点按逆时针方向旋转90，B点的位置恰好在△ABC的AC边所在的直线上。

你认为其中正确的有（　　）

A、0个　　　　 B、1个　　　　C、2个　　　D、3个

二. 认真填一填 (本题有5个小题, 每小题4分, 共20分)

　　要注意认真看清题目的条件和要填写的内容, 尽量完整地填写答案.

16、已知Rt_△ABC的两直角边AC、BC分别是一元二次方程x²－5x﹢6=0两根，则此Rt_△的外接圆的面积为　　　　　　　 。

17、一顶简易的圆锥形帐篷，帐篷收起来时伞面的长度有4米，撑开后帐篷高2米，则帐篷撑好后的底面直径是______________米.

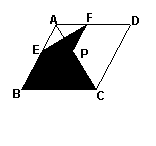
18、如图，菱形ABCD的对角线的长分别为2和5，P 是对角线AC上任一点

（点P不与点A、C重合）， 且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是　　　　　．

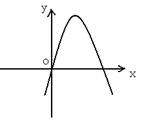
19、若二次函数y=ax²+2x+a²-1(a≠0)的图象如图（下右）所示,则a的值是____________.

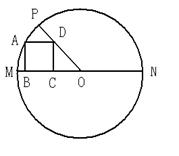
20、如图（下左），已知在⊙O中，直径MN=10，正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上，并且∠POM=45°，则AB的长为___________.

　　 

三. 全面答一答 (本题有6个小题, 共55分)

　　解答应写出文字说明, 证明过程或推演步骤. 如果觉得有的题目有点困难, 那么把自己能写出的解答写出一部分也可以.（7+8+8+10+10+12）

21(7分)、如图，点A、B、C在⊙O上，连结OC、OB：

（1）求证：∠A=∠B+∠C；

（2） 若点A在圆上移动（不与点B、C重合），请分析∠A、∠B、∠C三者之间的数量关系。（写出结论即可）

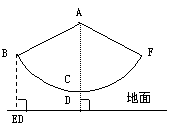
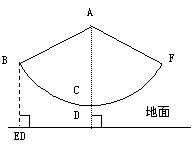
22(8分)．如图，秋千拉绳长AB为3米，静止时踩板离地面0.5米，

某小朋友荡该秋千时，秋千在最高处时踩板离地面2米(左右

对称)，请计算该秋千所荡过的圆弧长(精确到0.1米)？

23(8分)、有一农户用24米长的篱笆围成一面靠墙(墙长为10米),大小相等且彼此相连的三个矩形鸡舍,(如图所示)求鸡场面积的最大值是多少？

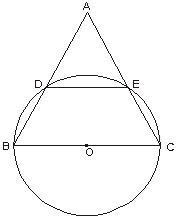
24(10分).如图，以等腰三角形ABC的底边BC直径的圆O分别交两腰于D、E，连结DE，求证：（1）DE//BC，（2）若D是AB中点，则△ABC是等边三角形。

　　　　　　　　　　　　　　　　　　　　　

25、（10分）

在一块长16m、宽12m的矩形荒地上，要建造一个花园，要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.

小明说：我的设计方案如图（1），其中花园四周小路的宽度相等. 通过解方程，我得到小路的宽为2m或12m.

小颖说：我的设计方案如图（2），其中花园中每个角上的扇形相同.

（1）你认为小明的结果对吗？请说明理由.

（2）请你帮助小颖求出图中的x（精确到0.1m）.

（3）你还有其他的设计方案吗？请在右边的矩形中画出你的设计草图，并加以说明.

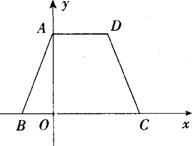26(12分)．已知：如图,等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A( 0, 6 )，D ( 4，6），且AB＝.

（1）求点B的坐标；

（2）求经过A、B、D三点的抛物线的解析式；

（3）在（2）中所求的抛物线上是否存在一点P，使得S△PBC　= S梯形ABCD　?若存在，请求出该点坐标，若不存在，请说明理由

2006学年第一学期期中考试

九年级数学答题卷

一. 仔细选一选 (本题有15个小题, 每小题3分, 共45分)

题号	1	2	3	4	5	6	7	8	9	10
答案
题号	11	12	13	14	15
答案

二. 认真填一填 (本题有5个小题, 每小题4分, 共20分)

16、　　　　 __________17、　　　　　 _________18、　　　　  ______

19、__________________ 20、　　　　 ___________

三. 全面答一答 (本题有6个小题, 共55分)

21、（本题7分）

22、（本题8分）

23、（本题8分）

24、（本题10分）

25、（本题10分）

　　　

26、（本题12分）

　 

.数学九年级参考答案

一. 仔细选一选 (本题有15个小题, 每小题3分, 共45分)

题号	1	2	3	4	5	6	7	8	9	10
答案	A	C	C	D	A	C	C	B	C	C
题号	11	12	13	14	15
答案	B	B	C	C	D

二. 认真填一填 (本题有5个小题, 每小题4分, 共20分)

16、　　13∏/4　　　　　　 17、　　　　　 18、　　　 5/2　　　　　 _

19、　　a=-1　　　　　　　 20、　　　　_　　

三. 全面答一答 (本题有6个小题, 共55分)

21、（本题7分）

　　　（1）略-------------4分

　　　（2）点A在圆上移动（不与点B、C重合）都是∠A=∠B+∠C----3分

22、（本题8分）

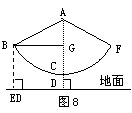解：如图，AD垂直地面于D并交圆弧于C，BE垂直地面于E.

根据题设，知BE=2，AC＝3，CD＝0.5(单位：米).  ------------------2分

作BG⊥AC于G，

则AG＝AD－GD＝AC＋CD－BE＝1.5.　---------------------------------------4分

由于AB＝3，

所以在直角三角形ABG中，∠BAG＝60°.   -------------------------------5分

根据对称性，知∠BAF＝120°.   ----------------------------------------------------6分

所以，秋千所荡过的圆弧长是(米).

答：(略).　---------------------------------------------------------------------------------------------8分

23、（本题8分）

　 解：设鸡场的总长为 x米，面积为y平方米

Y=X﹙24-x﹚/4

=-1/４(x-12) ²+36-----4分

　　　因为x=12不属于0＜x≤10 ,所以当x=10时y有最大值为35 平方米 ----------4分

　　

24、（本题10分）(1)

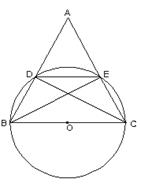连结CD，BE，

∵BC是直径，D，E在圆上

∴∠BDE=∠BCE=90

∵∠ABC=∠BCA，BC=BC

∴△BDE≌△BCE-------------------------3分

∴BD=CE

∴弧BD=弧CE

∴∠BED=∠EBC

∴DE∥BC------------------------------3分

(2) ∵CD⊥AB且BD=AD

　　　　　　　　　　　　 ∴BC=AC

∵AB=AC

　　　　　　　　　　　　  ∴BC=AB=AC

∴△ABC是等边三角形—--------4分

25(10分)．（1）设小路的宽为xm，则（16－2x）（12－2x）=×16×12，

解得x=2，或x=12（舍去）. ∴x=2，故小明的结果不对.-------- ------4分

　 （2）四个角上的四个扇形可合并成一个圆，设这个圆的半径为rm，

故有r²=×16×12，解得r≈5.5m.---4分

　 （3）依此连结各边的中点得如图的设计方案---2分

26、（本题12分）

（1）B（－2，0）--------2分

（2）抛物线的解析式为y= -x²+2x﹢6-------------4分

（3）(2+,9/2)、　(2-,9/2) 、 (7,-9/2) 、　(-3,-9/2)

------- 6分