九年级数学第一学期学生期末学业质量检测
试卷
注意:
1.本卷分试题卷和答题卷两部分. 试卷共三大题23小题,满分150分,考试时间100分钟.
2.答题时, 先在答题卷上写明校名,班级,姓名和学号.所有答案都做在答题卷标定的位置上, 务必注意试题序号和答题序号相对应.
一、 细心选一选 (本题有10个小题, 每小题4分, 满分40分) 下面每小题给出的四个选项中, 只有一个是正确的, 请把正确选项前的字母填在答题卷中相应的格子内.
1. 气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( ).
A.本市明天将有80%的地区降水 B.本市明天将有80%的时间降水
C.明天肯定下雨 D.明天降水的可能性比较大
2.
已知![]() 是一元二次方程
是一元二次方程![]() 的一个根,则
的一个根,则![]() 的值是( ).
的值是( ).
A. 0 B. 1 C. 2 D. -2
3. 下面计算错误的是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
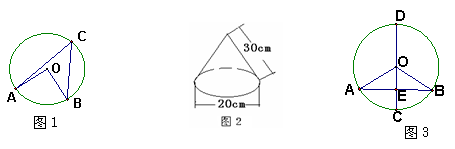
4.如图1,点A、B、C在⊙O上,且∠AOB=90°,则∠C的度数为( ).
A. 22.5° B. 30° C. 45° D. 60°
5. 如图2:是小明制作的一个圆锥型纸帽的示意图,则围成这个纸帽所用的纸的面积
为( )![]() (不计粘贴部分).
(不计粘贴部分).
 A. 150
A. 150![]() B. 300
B. 300![]() C. 400
C. 400![]() D. 600
D. 600![]()
6. 如图3,CD是⊙O的直径且CD=4,CD⊥AB于点E,∠A=30°,则弦AB的长为( ).
A.1 B.2
C.![]() D.
D.![]()
7.
一元二次方程![]() 的根的情况为( ).
的根的情况为( ).
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
8. 下面是作一项抽样调查时,所采用的选取样本的几种做法,其中合适的有( ).
①为了解200台洗衣机的质量,从中随机抽取20台进行检测;
②在公园里调查老年人的健康情况;
③为了解某班学生当天的数学作业的情况,老师批改了一个学生的数学作业.
A. 0种 B. 1种 C. 2种 D. 3种
 9.如图4,已知△ABC的三条边及三个角,则按照下面甲、乙、丙三个三角形所给的条件判断,能和△ABC全等的图形是( ).
9.如图4,已知△ABC的三条边及三个角,则按照下面甲、乙、丙三个三角形所给的条件判断,能和△ABC全等的图形是( ).
![]()
A.甲、乙 B.甲、丙 C.乙、丙 D.乙
10.已知⊙O1与⊙O2外切于点A,⊙O1的半径R=2,⊙O2的半径r=1,则与⊙O1、⊙O2相切,且半径为4的圆有( ).
A.2个 B.4个 C.5个 D.6个
二、耐心填一填 (本题有6个小题, 每小题4分, 共24分).
11. 要使分式![]() 有意义,则
有意义,则![]() 的取值范围是 .
的取值范围是 .
12. 一元二次方程![]() 的根为
.
的根为
.
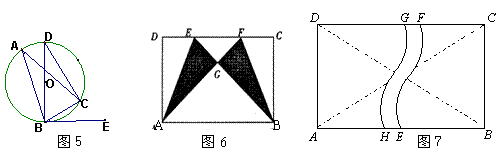 13. 已知:如图5,△ABC内接于⊙O,BD是⊙O的直径,BE切⊙O于点B,∠A=30°,则
13. 已知:如图5,△ABC内接于⊙O,BD是⊙O的直径,BE切⊙O于点B,∠A=30°,则
∠CBE= 度.
14. 某厂一月份生产某机器100台,计划三月份生产280台.设二、三月份每月的平均增长率为![]() ,根据题意列出的方程是____________________.
,根据题意列出的方程是____________________.
15.如图6,矩形ABCD中,![]() ,将∠D与∠C分别沿直线AE、BF向内折叠,使点D、C重合于点G,且
,将∠D与∠C分别沿直线AE、BF向内折叠,使点D、C重合于点G,且![]() ,则
,则![]() .
.
16.如图7,矩形草坪ABCD中,AD=10m,AB=![]() m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积是_______________
m2. (结果保留
m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积是_______________
m2. (结果保留![]() )
)
三、用心答一答 (本题有7个小题, 共86分, 解答要求写出文字说明, 证明过程或计算步骤)
17. (本题满分10分)化简: (![]() +
+![]() )÷
)÷![]() .
.
18. (本题满分20分)(1)解分式方程: ![]()
(2)用配方法解方程: ![]()
19. (本题满分10分)
已知:如图8,点C、D在线段AB上.请你从下面三个选项中选出两个作为条件,另一个作为结论,写出一个真命题,并给予证明.
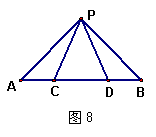
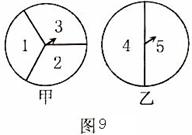 (1)PA=PB (2)PC=PD (3) AC=BD .所添条件为: ∠A=∠B(或PA=PB或AC=BD或AD=BC或∠APC=∠BPD或∠APD=∠BPC等)
(1)PA=PB (2)PC=PD (3) AC=BD .所添条件为: ∠A=∠B(或PA=PB或AC=BD或AD=BC或∠APC=∠BPD或∠APD=∠BPC等)
全等三角形为:△PAC≌△PBD(或△APD≌△BPC)
证明:(略)
20.(本题满分10分)
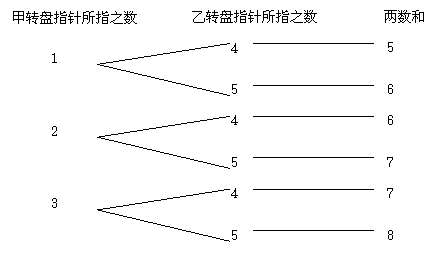
如图9,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题。
⑴ 在图甲中,随机地转动指针,指针指向扇形1的概率是______________;
在图乙中,随机地转动指针,指针指向扇形4的概率是______________;
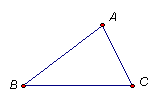 ⑵ 随机地转动图甲和图乙指针,则两个指针所指区域内的数之和为6或7的概率是______________,请用一种合适的方法(例如:树状图,列表)计算概率.
⑵ 随机地转动图甲和图乙指针,则两个指针所指区域内的数之和为6或7的概率是______________,请用一种合适的方法(例如:树状图,列表)计算概率.
![]() 21.(本题满分10分)
21.(本题满分10分)
已知:△ABC(如图10)
求作:作△DBC,使△DBC和△ABC全等,请作出所有满足条件的全等三角形.
(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明).
22.(本题满分12分)
老师给小明出了一道题,小明感到有困难,请你帮助小明解决这个问题.题目是这样的:一个三角形两边长分别是3和4,第三边长是![]() 的一个实数根,请画出所有情况的示意图并且求出其中一个三角形的外接圆面积.
的一个实数根,请画出所有情况的示意图并且求出其中一个三角形的外接圆面积.
23.(本题满分14分)
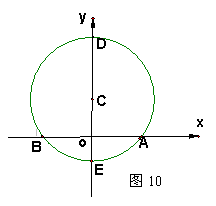
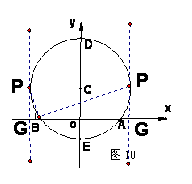
已知:如图11,在平面直角坐标系中,点C的坐标为(0,2),以C为圆心,以4为半径的圆与x轴相交于点A、B,与y轴相交于点D、E.
(1) 请求出A、B两点的坐标;
(2)
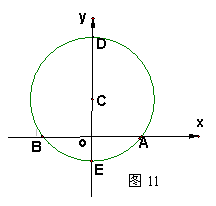 若点P是弧ADB上一动点(P点与A、B点不重合)连结BP、AP.问当点P移到何处时,△APB的面积最大?并求出这时△APB的面积;
若点P是弧ADB上一动点(P点与A、B点不重合)连结BP、AP.问当点P移到何处时,△APB的面积最大?并求出这时△APB的面积;
(3) 若⊙C的切线PG交x轴于点G,是否存在这样的点,
使△BPG是直角三角形?若存在,请求出所有符合条件
的点P的坐标;若不存在,请说明理由.
|
九年级数学答题卷
| 题 号 |
一 |
二 | 三 | 总 分 | ||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23
| ||||
| 得 分 |
|
|
|
|
|
|
|
|
|
|
一、 细心选一选 (本题有10个小题, 每小题4分, 满分40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、 耐心填一填 (本题有6个小题, 每小题4分, 共24分)
| 题号 | 答案 | 题号 | 答案 |
| 11 |
| 14 |
|
| 12 |
| 15 |
|
| 13 |
| 16 |
|
三、用心答一答 (本题有7个小题, 共86分)
| 17、(本题满分10分) 解: | |
| 18、(本题满分20分) 解:(1) | 解:(2) |
| 19、(本题满分10分) 命题:如果 ,那么 .
| |
| 20、(本题满分10分) 解:⑴ 在图甲中,随机地转动指针,指针指向扇形1的概率是______________; 在图乙中,随机地转动指针,指针指向扇形4的概率是______________ ⑵概率是______________ 21、(本题满分10分)
| |
| 22、(本题满分12分) 解: | |
| 23、(本题满分14分) 解:(1)
(3) \ | |
九年级数学第一学期学生期末学业质量检测评分标准
三、 细心选一选 (本题有10个小题, 每小题4分, 满分40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | C | C | B | C | A | B | C | D |
四、 耐心填一填 (本题有6个小题, 每小题4分, 共24分)
| 题号 | 答案 | 题号 | 答案 |
| 11 |
| 14 |
|
| 12 |
| 15 | 2 |
| 13 | 30 | 16 |
|
注意:第12题写成“0或4”不扣分。
三、用心答一答 (本题有7个小题, 共86分)
| 17、(本题满分10分) 解:
第一步只算对括号得4分 | |||||||||||||
| 18、(本题满分20分) 解:(1)
| 解:(2)
| ||||||||||||
| 19、(本题满分10分) (1)命题:如果 PA=PB,AC=DB ,那么 PC=PD .…………2分
∴∠A=∠B…………5分 又∵AC=DB ∴△PAC≌△PBD…………8分 ∴PC=PD …………10分 (2)命题:如果 PA=PB, PC=PD ,那么 AC=DB .…………2分
∴∠A=∠B …∠PCD=∠PDC………5分 ∴∠PCA=∠PDB ……7分 ∴△PAC≌△PBD…………8分 ∴PC=PD …………10分 (3) 命题:如果 AC=DB , PC=PD ,那么 PA=PB .…………2分
∴∠PCD=∠PDC………5分 ∴∠PCA=∠PDB ……6分 ∵AC=DB ∴△PAC≌△PBD…………8分 ∴PA=PB …………10分 | |||||||||||||
| 20、(本题满分10分) 解:⑴ 在图甲中,随机地转动指针,指针指向扇形1的概率是______ 在图乙中,随机地转动指针,指针指向扇形4的概率是_________ ...................................4分 ⑵概率是________ 两数和为6或7的概率为P= 树状图如下:
或列表
三种方法,画一种得4分,画全给10分,看痕迹给分 大概位置如图所示 | |||||||||||||
| 22、(本题满分12分) 解:解 (1) 若 示意图1分..........6分
R= S= (2)若 R= S=
面积只需计算一种得4分, | |||||||||||||
|
解:(1)连结AC,BC,依题意得:AC=BC=4,OC=2 OA=OB= 点A坐标为( 点B坐标为(- (2)当点P移到点D时,△APB的面积最大. .......5分 这时 △APB的面积= ........7分
1)当 则点P坐标为(4,2)或(-4,2) ........10分 2)当 则AP是直径,AP=8, 点P坐标为(- 3)当 点P坐标为( 或者AP是直径,同2)点P坐标为(-
| |||||||||||||
 证明:
证明:
 (2)
(2)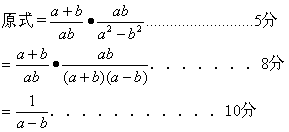

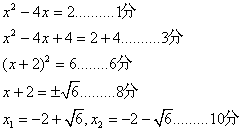
 。。。。。。。。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。。。。。。。。10分 乙
乙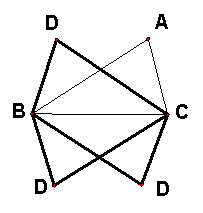 21、(本题满分10分)
21、(本题满分10分) 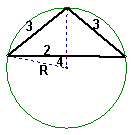 设半径为R,则有
设半径为R,则有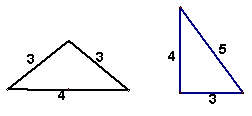
 (3)存在。 ........8分
(3)存在。 ........8分 所以符合条件的点P坐标为(4,2)或(-4,2) 或(-
所以符合条件的点P坐标为(4,2)或(-4,2) 或(-