九年级(上)数学期末综合测试（2）

九年级(上)数学期末综合测试（2）

　　　　　　　　 

一、选择题：（30分）

1、（2004·重庆）化简的结果为　　　　　　　　　　　 （　 ）

　A、　　  B、　　　　C、　　  D、

2、（2004·淄博）若关于x的一元二次方程有实数根，则k的取值范围是（　）

Ａ　k＞－1　 　Ｂ k≥－1　　 Ｃ k＞－1且k≠0　 　　 Ｄ k≥－1且k≠0

3、关于的一元二次方程的一个根是0，则的值为　　　 （　 ）

A、1　　　　　 B 、-1　　　　 C、1或-1　　　　D、0.5

4、有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”，“08”和“北京”的字块，如果婴儿能够排成“2008北京”或者“北京2008”，则他们就给婴儿奖励。假设婴儿能将字块横着正排，那么这个婴儿能得到奖励的概率是 　　　　 (　　).

A．　　　　　 B．　　　　　  C．　　　　　　 D．

5、已知关于x的一元二次方程x²－2 (R＋r) x＋d²＝0没有实数根，其中R，r分别为⊙O₁，⊙O₂的半径，d为两圆的圆心距，则⊙O₁与⊙O₂的半径，d为两圆的圆心距，则⊙O₁与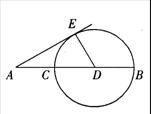⊙O₂的位置关系是 (　　 ).

 A．外离　　　　B．相交　　　　C．外切　　　　 D．内切

6、如图，AE切⊙D于点E，AC＝CD＝DB＝10，则线段AE的长为（  ）．

A 　　B 15 　　　 C 　　 D 20　　

7、（06天门）老师出示了小黑板上的题后(如图)，小华说：过点(3，0)； 小彬说：过点(4，3)；小明说：a=1；小颖说：抛物线被x轴截得的线段长为2。你认为四人的说法中，正确的有（　　）

A、1个　　 B、2个　　 C、3个　　 D、4个

8、如图，AB、CD是⊙O的直径，⊙O的半径为R,AB⊥CD，以B为圆心，以BC为半径作C⌒ED，则C⌒ED与C⌒AD围成的新月形ACED的面积为（　 ）平方单位．

A．　B．　C．　 D．

9、将一图形绕着点O顺时针方向旋转70⁰后，再绕着点O逆时针方向旋转120⁰，这时如果要使图形回到原来的位置，需要将图形绕着点O什么方向旋转多少度？　（　　 ）

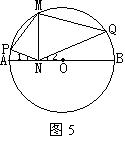A、顺时针方向　50⁰　　　　 B、逆时针方向　　50⁰

C、顺时针方向　 190⁰　　　 D、逆时针方向　　190⁰

10、如图5，AB是⊙O的直径，M是⊙O上一点，MN⊥AB，垂足为N，P、Q分别是AM、BM上一点（不与端点重合），如果∠MNP=∠MNQ，下面结论：①∠1=∠2；②∠P+∠Q=∠180°；③∠Q=∠PMN；④PM=QM；⑤MN²=PN·QN。其中正确的是（　）

A．①②③　　B．①③⑤　　C．④⑤　　D．①②⑤

二、填空题：（30分）

11、函数中，自变量的取值范围是　　　　　　　 .

12、（06荆门）化简:=________.

13、已知实数a，b，c满足， 则a＋b＋c =　__________。

14、在Rt△ABC中，∠C=90°，斜边AB=，两直角边a、b的长是方程x²－(m+1)x+m=0的两根,则m=　　　　 .

15、半径分别为4和5的相交两圆所成的公共弦长为6，则两圆的圆心距为________.

16、雨后初晴，一个学生在运动场上玩耍，在他前面2m远处有一块小积水，他看到了旗杆的倒影。若旗杆底端到积水处的距离为40m，该生的眼部高度为1.5m，则旗杆的高度是　　　　　　  　　 m。

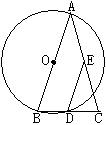
17、已知：如图，等腰三角形ABC中，AB=AC=4，若以AB为直径的⊙O与BC相交于点D，DE∥AB，DE与AC相交于点E，则DE=________。

18、已知函数的图象关于y轴对称，则m＝________

19、有一条抛物线，三位学生分别说出了它的一些性质：

　 甲说：对称轴是直线x=2；乙说：与x轴的两个交点距离为6；

　 丙说：顶点与x轴的交点围成的三角形面积等于9，请你写出满足

　 上述全部条件的一条抛物线的解析式：　　　　　　　　

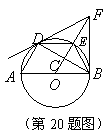
20、由⊙O外一点作⊙O的两条切线，切点为是⊙O的直径，　　 连结，交⊙O于，交于，连结．下列四个结论：① ②③ ④BD²=2AD·FC其中正确的结论有　　　　　　　 （把你认为正确结论的序号全部填上）．

三、解答题：（60分）

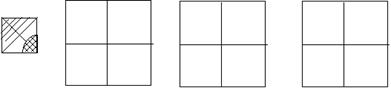
21、(6分)用四块如图1所示的正方形瓷砖拼成一个新正方形，使拼成的图案是一个轴对称图形.请你在图2、图3、图4中各画一种拼法（要求三种拼法各不相同，且其中至少有一个图形既是轴对称图形，又是中心对称图形）.

22、（7分）如图，在一个横截面为Rt△ABC的物体中，∠ACB＝90°,∠CAB＝30°,BC＝1米.工人师傅要把此物体搬到墙边，先将AB边放在地面（直线l）上,再按顺时针方向绕点B翻转到△A₁BC₁位置（BC₁在l上），最后沿BC₁的方向平移到△A₂B₂C₂的位置，其平移的距离为线段AC的长度（此时A₂C₂恰好靠在墙边）。

（1）请直接写出AB, AC的长；

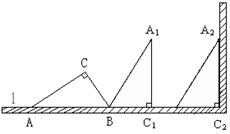（2）画出在搬动此物的整个过程A点所经过的路径，并求出该路径的长度。

23、（8分）某商场设立了一个可以自由转动的转盘,并规定：顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据：

(1)计算并完成表格：

(2)请估计,当n很大时,频率将会接近多少？

(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少？

(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少(精确到1°)

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”的次数m	68	111	136	345	564	701
落在“铅笔”的频率

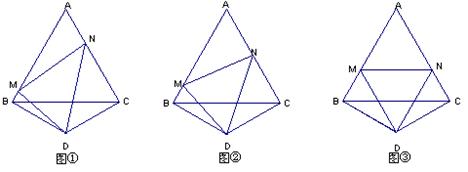
24、（10分）操作：如图①，△ABC是正三角形，△BDC是顶角∠BDC＝120°的等腰三角形，以D为顶点作一个60°角，（1）角的两边分别交AB、AC边于M、N两点，连接MN．

探究：线段BM、MN、NC之间的关系，并加以证明．

说明：⑴如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；⑵在你经历说明⑴的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．注意：选取①完成证明得6分；选取②完成证明得4分．

①（如图②）；　　②（如图③）．

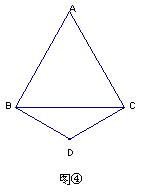（2）若点M、N分别是射线AB、CA上的点，其它条件不变，再探线段BM、MN、NC之间的关系，在图④中画出图形，并说明理由．　　

25、（7分）已知一个二次函数的图象经过A(－1,0),B(0,3),C(4,－5)三点.(1)求这个函数的解析式及其顶点D的坐标; (2)这个函数的图象与轴有两个交点,除点A外的另一个交点设为E,点O为坐标原点,在△AOB、△BOE、△ABE和△DBE这四个三角形中,是否有相似三角形?如果有,指出哪几对三角形相似,并加以证明;如果没有,请说明理由。

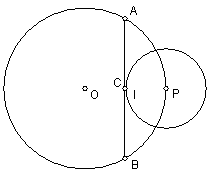
26、（10分）已知⊙O的半径为R，⊙P的半径为r（r<R），且⊙P的圆心P在⊙O上。设C是⊙P上一点，过点C与⊙P相切的直线交⊙O于A、B两点。

(1)若点C在线段OP上，（图1），求证：PA·PB=2Rr；

(2)若点C不在线段OP上，但在⊙O的内部，（图2）。此时，（1）中的结论是否成立？若成立，请给予证明；如不成立，说明理由；

(3)若点C在⊙O的外部，（图3）。此时，PA·PB与R，r的关系又如何？请直接写出结论，不要求给予证明或说明理由。

　

　

 

27、（12分）直线l的解析式为，与x轴、y轴分别交于A、B两点，P是x轴上一点，以P为圆心的圆与直线l相切于B点。

（1）求点P的坐标及⊙P的半径R；

（2）若⊙P以每秒个单位沿x轴向左运动，同时⊙P的半径以每秒个单位变小，设⊙P的运动时间为t秒，且⊙P始终与直线l有交点，试求t的取值范围；

（3）在(2)中，设⊙P被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t的值；

（4）在(2)中，设⊙P与直线l的一个交点为Q，使得△APQ与△ABO相似，请直接写出此时t的值。

参考答案

1、A　　　　　　 2、D　　　　　　 3、B　　　　　　 4、C　　　　　　 5、A

6、C　　　　　　 7、D　　　　　　 8、B　　　　　　 9、A　　　　　　 10、B

11、x≤2且x≠1　　　　　　　 12、2　　　　　　　　　　　　　　　　 13、8或11

14、2　　　　　　　　　　　　　　　　 15、4+或4－

16、30　　　　　　　　　　　　　　　 17、2

18、1　　　　　　　　　　　　　　　　 19、y= x²－－或y=－x²＋＋

20、①②④

21、略

22、（1）AB＝2米， AC＝米

（2）A点所经过的路径如右图。解：∠ACB＝90°,

∠CAB＝30°

∴由题图可知∠A₁BC₁＝90°－30°＝60°

∴∠ABA₁＝120°

∴⌒AA₁＝＝ π

∵ AA₂＝

∴A点所经过的路径的长为（ π＋）米。

23、解：（1）

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”的次数m	68	111	136	345	564	701
落在“铅笔”的频率	0.68	0.74	0.68	0.69	0.705	0.701

（2）当n很大时,频率将会接近0.7；

（3）获得铅笔的概率约是0.7；

（4）扇形的圆心角约是

24、（1）BM＋CN＝MN　

 证明：如图，延长AC至M₁，使CM₁＝BM，连结DM₁

由已知条件知：∠ABC＝∠ACB＝60°，∠DBC＝∠DCB＝30°∴∠ABD＝∠ACD＝90°

∵BD＝CD ∴Rt△BDM≌Rt△CDM₁

∴∠MDB＝∠M₁DC　　DM＝DM₁

∴∠MDM₁＝（120°－∠MDB）＋∠M₁DC＝120°

又∵∠MDN＝60°

∴∠M₁DN＝∠MDN＝60°　　 ∴△MDN≌△M₁DN 

∴MN＝NM₁＝NC＋CM₁＝NC＋MB

（2） CN－BM＝MN

证明：如图，在CN上截取，使CM₁＝BM，连结DM₁分

∵∠ABC＝∠ACB＝60°，∠DBC＝∠DCB＝30°

∴∠DBM＝∠DCM₁＝90°

∵BD＝CD　　　∴Rt△BDM≌Rt△CDM₁

∴∠MDB＝∠M₁DC　DM＝DM₁　

∵∠BDM＋∠BDN＝60°

∴∠CDM₁＋∠BDN＝60°

∴∠NDM₁＝∠BDC－（∠M₁DC＋∠BDN）

＝120°－60°＝60°

∴∠M₁DN＝∠MDN　

∵AD＝AD ∴△MDN≌△M₁DN

∴MN＝NM₁＝NC－CM₁＝NC－MB　

 

25、（1）y=－x²+2x+3　 D(1,4)

（2）△AOB∽△DBE可求出三角形各边长,对应的边的比相等

26、（1）作⊙O的直径PD，连结BD，PA=PB证明△PAC∽△PDB

可得PA·PB=PC·PD=r·2R

（2）与（1）同理，证明△PAC∽△PDB

（3）与（1）同理，证明△PAC∽△PDB。

27、（1）P(6,0)　R=10;

(2)0≤t≤40/7;

(3)t=5;

(4) t=40/7