九年级数学试题卷
一. 选择题 (本题有10个小题, 每小题4分, 共40分)
1．当x=1时，代数式2x+5的值为( )
（A）3 （B）5 (C ) 7 （D）－2
2．下列计算正确的是（ ）．
（A）（ab）2=ab2 （B）a5+a5=2a5 (C ) a2·a3=a4 （D）（a2）3=a5
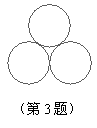
3．如图是叠靠在一起的三根塑料管横截面示意图，它们表示的圆与圆
之间位置关系是（ ）．
（A）外切 （B）内切 （C）相交 （D）外离
4. 反比例函数
的图象在每个象限内，
随
的增大而减小，则
的值 可为（ ）
（A）
（B）0
(C ) 1
（D）2
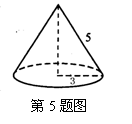
5．如图，圆锥的母线长为5cm，底面半径为3cm，则此圆锥的高线长为（ ）
(A) 4cm (B) 5cm (C) 3cm (D) 8cm
6. 三角形的两边长分别为3和6，第三边的长是方程x2－6x＋8＝0的一个根，
则这个三角形的周长是（ ）
（A）9 （B）11 （C）13 （D）11或13
7．不等式组
的解集在数轴上可以表示为（
）
（A）
（B）
（C）
（D）
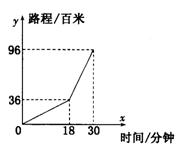
8.小亮早晨从家骑车到学校，先上坡后下坡，行程情况如图所
示．若返回时上坡、下坡的速度仍保持不变，那么小明从学
校骑车回家用的时间是（ ）
( A ) 37.2分钟 (B) 48分钟
(C ) 30分钟 ( D )33分钟
9．如图，四边形ABCD是由四个边长为1的正六边形所围成，则四边形ABCD的面积是（ ）
（A）
（B）
（C）1 （D）2
10. 已知∠BAC=450 ,一动点O在射线AB上运动(点O与点A不重合), 设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是( )
(A)O<x≤
(B)1< x≤ (C)1≤x<
(D)x>
二. 填空题(本题有6个小题, 每小题5分, 共30分)
11．在函数y=
有表达式中，自变量x的取值范围是
。
12．分解因式：2x2+4x+2= 。
13．如图，DE是ΔABC的中位线，则ΔADE与ΔABC的周长之比是 。
14.一射击运动员在一次射击练习中打出的成绩如下表所示：这次成绩的众数是 。
| 成绩(环) | 6 | 7 | 8 | 9 | 10 |
| 次数 | 2 | 5 | 6 | 4 | 3 |
15.化简(
＋
)÷
的结果是
．
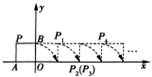
16. 如图，将边长为1的正方形OAPB沿x轴正方向连续翻转2 007次，点P依次落在点P1, P2, P3, P4, …，P2 007的位置，则P2 007 的横坐标x2 007＝_______
三. 解答题(本题有8小题，共80分)
17.
(本题10分)(1) 计算：
(2) 解方程
.
 |
18．（本题8分）已知：如图，在四边形ABCD中， AD∥BC，AB＝CD，
过点D作DE∥AB，交BC于点E.
(1) 请你判断：线段DE把四边形ABCD分成两个图形，
其中四边形ABED是 四边形,三角形DEC是 三角形；
(2)请选择以上你所判断的其中一个结论加以证明.
求证：
证明：
19. (本题8分)已知一次函数的图象经过（2，5）和（－1，－1）两点．
（1）在给定坐标系中画出这个函数的图象；
（2）求这个一次函数的解析式．
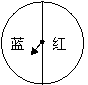
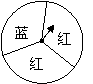
20．(本题8分)小颖为九年级8班毕业联欢会设计了一个“配紫色”的游戏：下面是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形．游戏者同时转动两个转盘，两个转盘停止转动时，若有一个转盘的指针指向蓝色，另一个转盘的指针指向红色，则“配紫色”成功，游戏者获胜．求游戏者获胜的概率．
 | |||
 | |||
21．(本题lO分) 一位华侨回乡访祖观光.他驱车游玩，在如图的一条南北走向的公路
上，汽车自A处由南向北前行时，车载GPS（全球卫星定位系统）显示石笋C在他西北方向上，他继续向北前进4千米到达B时，发现石笋C在他南偏西60°的方向上。
（1）试在图形上作出从石笋C到公路
的最短路径；
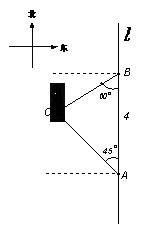（2）求出石笋C到公路的最短路径约为多少千米？（结果精确到0.1千米）
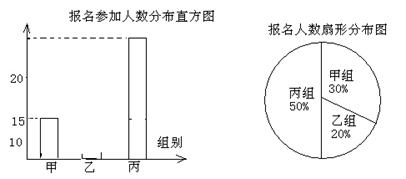
22．(本题lO分) 某年级组织学生参加夏令营活动，本次夏令营分为甲、乙、丙三组进行。下面两幅统计图反映了学生参加夏令营的报名情况，请你根据图中的信息回答下列问题：(1)该年报名参加丙组的人数为 ；
(2)该年级报名参加本次活动的总人数为 ，并补全频数分布直方图；
(3)根据实际情况，需从甲组抽调部分同学到丙组，使丙组人数是甲组人数的3倍，应从甲抽调多少人名学生到丙组？
23.(本小题满分12分)
近阶段国际石油价格猛涨，中国也受其影响.为了降低运行成本，部分出租车公司
将出租车由使用汽油改装为使用液化气. 假设一辆出租车日平均行程为300千米.
（1）使用汽油的出租车，当前的汽油价格为4.6元／升. 假设每升汽油能行驶12千米，
行驶t天所耗的汽油费用为w元，请写出w关于t的函数关系式；
（2）使用液化气的出租车，当前的液化气价格为4.95元／千克. 假设每千克液化气能行驶15千米，行驶t天所耗的液化气费用为p元，请写出p关于t的函数关系式；
（3）若出租车要改装为使用液化气，每辆需配置成本为8000元的设备.根据近阶段汽油和液化气的价位，在（1）、（2）的基础上，问需要几天才能收回改装成本？
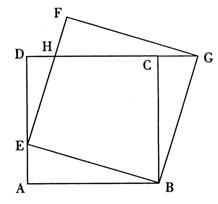
24.(本小题满分14分) 如图，正方形ABCD的边长为1，点E是AD边上的动点，从点A沿AD向D运动，以BE为边，在BE的上方作正方形BEFG，连接CG。请探究：
（1）线段AE与CG是否相等？请说明理由：
（2）若设
，
，当取何值时，最大？
（3）连接BH，当点E运动到AD的何位置时，△BEH∽△BAE？
