一元二次方程及其解法

练习七　　一元二次方程及其解法

一、选择

1、下列方程中,常数项为零的是　　　　　　　　　　　　　　　　  (　　 )

A、x²+x=1　　　　  B、2x²-x-12=12　　　C、2(x²-1)=3(x-1)  　　D、2(x²+1)=x+2

2、已知ｍ是方程ｘ²－ｘ－１＝０的一个根，则代数ｍ²－ｍ的值等于 （　　 ）

A、１　　　　　　B、－１　　　　 C、0　　　　　　　D、2

3、下列方程:①x²=0,② -2=0,③2+3x=(1+2x)(2+x),④3-=0,⑤-8x+ 1=0中,一元二次方程的个数是　　　　　　　　　　　　　　　　　　　  (　 　)

A、1个　　B、2个　　C、3个　　D、4个

4、方程x（x+1）=3（x+1）的解的情况是　　　　　　　　　　　　　 （　　）

A、x=-1　　　 B、x=3　　 C、　 D、以上答案都不对

二、填空

5、把方程4 —x² = 3x化为ax² + bx + c = 0(a≠0)形式为　　　　　　　　  ，则该方程的二次项系数、一次项系数和常数项分别为　　　　　　　　　　　　　　 。

6、在关于x的方程(m-5)x^m-7+(m+3)x-3=0中:当m=_____时，它是一元二次方程；当m=_____时，它是一元一次方程。

7、方程的解为　　　　　　　　　　　 ．

8、已知关于x的一元二次方程x²+kx+k=0的一个根是–2，那么k=____。

9、已知y=x²-2x-3，当x=　　　　 时，y的值是-3。

10、若方程有整数根，则的值可以是_________（只填一个）。

三、解答

11、解下列方程

（1）x²－4x+4=0　　　　　　　　　　　　　　　　　　　　　　（2）8y²－2=4y（配方法）

（3）2（2x－3）²－3（2x－3）=0　　　　　  （4）x²－（1+2）x+－3=0

　　　　　　　　 

12、如果一元二次方程x²＋ax ＋b= 0的两个根是0和—2，则a、b分别等于多少？

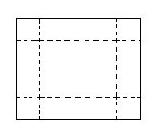
13、如下图，用一块正方形纸板，在四个角上截去四个相同的边长为2厘米的小正方形，然后把四边折起来，做成一个没有盖的长方体盒子，使它的容积为32立方厘米。所用的正方形纸板的边长应是多少厘米？（仅列方程，不求出解）

14、已知下列n（n为正整数）个关于x的一元二次方程：

　　　

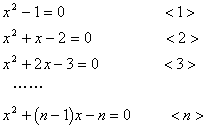
　　　 （1）请解上述一元二次方程<1>、<2>、<3>、<n>；

　　　 （2）请你指出这n个方程的根具有什么共同特点，写出一条即可。

答案：

一、D、A、A、C

二、5、x² + 3x —4=0， 1、3、—4；　　　　　　　　　 6、9、8；　　　　　　　　　 7、0、4；

8、4；　　　　　　　9、0、2；　　　　　　　 10、例如m=0，1，4，9，……

三、11、（1）x₁=x₂=2；（2）原方程没有实数解；(3)x₁=，x₂=；（4）x₁=3+，x₂=－2+

12、－2、0

13、方法一：设宽为xcm，则长为(x+5)cm，列方程 x(x+5)=150 ，化简得x² +5x =150 ；

方法二：设长为xcm，则宽为(x—5)cm，列方程 x(x—5)=150，化简得x²—5x =150 ；

14、（1）<1>，所以

　　　 <2>，所以

　　　 <3>，所以

　　　　　　　……

　　　 <n>，所以………………4分

（2）比如：共同特点是：都有一个根为1；都有一个根为负整数；两个根都是整数根等。