圆的期末复习检测试题 (基础卷)
一、精心选一选（每小题3分，共30分）
1．下列三个命题：①圆既是轴对称图形又是中心对称图形；②垂直于弦的直径平分弦；③ 相等的圆心角所对的弧相等．其中真命题的是（ ）
A.①② B. ②③ C. ①③ D. ①②③
2．⊙O的半径为4，圆心O到直线l的距离为3，则直线l与⊙O的位置关系是（ ）
A.相交 B.相切 C.相离 D.无法确定
3． ⊙O中，AOB＝∠84°，则弦AB所对的圆周角的度数为（ ）
A.42° B.138° C.69° D.42°或138°
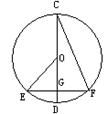
4．如图1，⊙O的直径CD垂直于弦EF，垂足为G，若∠EOD=40°,则∠DCF等于（ ）
A.80° B. 50° C. 40° D. 20°
5．已知两圆的半径是方程
两实数根，圆心距为8，那么这两个圆的位置关系是（ ）
A.内切 B.相交 C.外离 D.外切
6．已知圆上的一段弧长为5πcm，它所对的圆心角为100°,则该圆的半径为( )
A.6 B.9 C.12 D.18
7．两个圆是同心圆，大、小圆的半径分别为9和 5，如果⊙P与这两个圆都相切，则⊙P 的半径为( )
A.2 B.7 C.2或7 D.2或4.5
8．如图2，AB与⊙O切于点B，AO＝6㎝，AB＝4㎝，则⊙O的半径为（ ）
A、4
㎝ B、2㎝ C、2
㎝ D、㎝
9．如图3，已知⊙0的直径AB与弦AC的夹角为35°，过C点的切线PC与AB的延长线交于点P，则么∠P等于（ ）
A．150 B．200 C．250 D．300
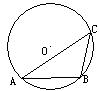
10．如图4，△ABC内接于⊙O，∠C=45°，AB= 4 ，则⊙O半径为（ ）
A、
B、4
C、
D、5
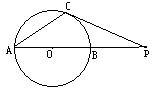
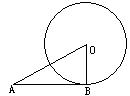
图1 图2 图3 图4
二、耐心填一填（每小题4分，共24分）
11．过⊙O内一点M的最长弦为10cm，最短弦为8cm，则OM= cm.．
12．Rt△ABC中，∠C＝90°，AC=5,BC=12,则△ABC的内切圆半径为 ．
13．已知正n边形的一个外角与一个内角之比为1︰3，则n等于 ．
14．某校九（3）班在圣诞节前，为圣诞晚会制作一个圆锥形圣诞老人的纸帽，已知圆锥的母线长为30cm，底面直径为20cm，则这个纸帽的表面积为 ．
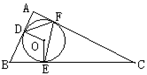
15．如图5，⊙O是△ABC内切圆，切点为D、E、F，∠A=100°，∠C=30°，则∠DFE度数是 ．
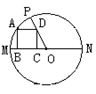16．如图6，⊙O中，直径为MN ，正方形ABCD四个顶点分别在半径OM、OP以及⊙O上，并且∠POM = 45°，若AB＝1，则该圆的半径为 ．
图5 图6
三、思维大比拼（17题6分，22、24题各10分，18、19、20、21、23题各8分，共66分）
17． 如图7，在△ABC中，∠ACB＝90°，∠B＝36°，以C为圆心，CA为半径的圆交AB于点D,交BC于点E.求 、 的度数．
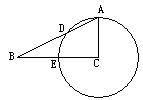
18．已知：如图8，△ABC中，AC＝BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．（8分）
求证：（1）AD＝BD； （2）DF是⊙O的切线．
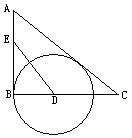19．如图9，在Rt△ABC中，∠B＝90°，∠A的平分线与BC相交于点D,点E在AB上，DE=DC,以D为圆心，DB长为半径作⊙D．（1）AC与⊙D相切吗？并说明理由．（2）你能找到AB、BE、AC之间的数量关系吗？为什么？
20．如图10，P是⊙O外的一点，PA、PB分别与⊙O相切于点A、B，C是 上的任意一点，过点C的切线分别交PA、PB于点D、E.
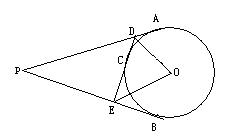(1)若PA=4,求△PED的周长；
(2)若∠P=40°,求∠DOE的度数．
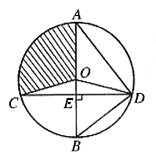
21．如图11，已知⊙O的直径AB垂直于弦CD于E，连结AD、BD、OC、OD，且OD＝5．
（1）若
，求CD的长；
（2）若
∠ADO：∠EDO＝4：1，求扇形OAC（阴影部分）的面积（结果保留
）．
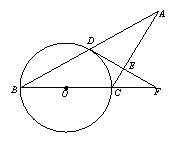
22．如图①，△ABC内接于⊙0，且∠ABC＝∠C，点D在弧BC上运动．过点D作DE∥BC．DE交直线AB于点E，连结BD．
(1)求证：∠ADB=∠E；
(2)求证：AD2=AC·AE；
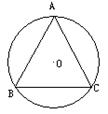
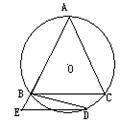(3)当点D运动到什么位置时，△DBE∽△ADE请你利用图②进行探索和证明．
图① 图②
23．图①是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形．图②是车棚顶部截面的示意图， 所在圆的圆心为O．
 |
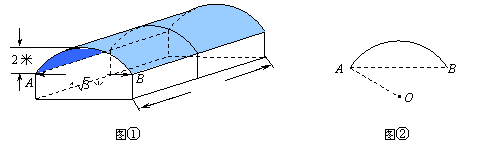车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积（不考虑接缝等因素，计算结果保留
）．
24．如图12，在直角梯形ABCD中，AD∥BC，∠B = 90°，AB =8㎝，AD=24㎝，BC=26㎝，AB为⊙O的直径。动点P从A点开始沿AD边向点D以1 cm/s的速度运动，动点Q从点C开始沿CB边向点B以3cm/s 的速度运动，P、Q 两点同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为 t s ,求：
（1） t分别为何值时，四边形PQCD为平行四边形、等腰梯形？
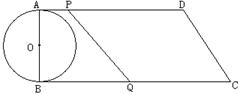（2） t分别为何值时，直线PQ与⊙O相交、相切、相离？
圆的检测（基础卷）参考答案
一、精心选一选
1.A 2.A 3.D 4.D 5.C 6.B 7.C 8.B 9.B 10.A
二、耐心填一填
11．3 12．2
13．8 14．300
15．65° 16．
三、思维大比拼
17． 、 的度数分别为72°、18°；
18．略
19．（1）相切 （2）AB+BE=AC
20．（1）8 （2）70°
21．（1）CD=9.6 （2）扇形OAC的面积为
．
22．（1）略 （2）略 （3）当D运动到弧BC的中点时，△DBE∽△ADE．
23．160平方米
24．（1）当t =6时，四边形PQCD为平行四边形；当t =7时，四边形PQCD为等腰梯形．
（2）当t =
或8时，直线PQ与⊙O相切； 当0≤t﹤或8﹤t≤
时，直线PQ与⊙O相交；
当﹤t﹤8时，直线PQ与⊙O相离．