圆基础题精选二
一、填空题
1.如果⊙O的半径为r，点P到圆心O的距离为d，那么：①点P在⊙O外，则______；②______则d=r；③______则d<r.
2.两个同心圆的直径分别为5 cm和3 cm，则圆环部分的宽度为_____ cm.
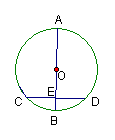
3.如图1,已知⊙O，AB为直径，AB⊥CD，垂足为E，由图你还能知道哪些正确的结论?请把它们一一写出来. .
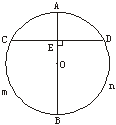
图1
4.如果把人的头顶和脚底分别看作一个点，把地球赤道看作一个圆，那么身高2 m的小赵沿着赤道环行一周，他的头顶比脚底多行_____m.
5.如图2，AB是⊙O的直径，C为圆上一点， =60°，OD⊥BC，D为垂足，且OD=10，则AB=_____，BC=_____.
6.如图3，⊙O中，已知
=
，且∶ =3∶4，则∠AOC=_____.
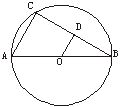
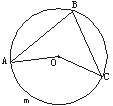
图2 图3
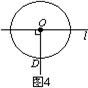
7.如图4,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移______cm时与⊙O相切.
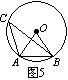
8.如图5,∠C是⊙O的圆周角,∠C=38°,∠OAB=______度.
9.两圆的半径分别为3cm和4cm,圆心距为5cm,则两圆的位置关系为______.
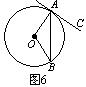
10.如图6,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于______时,AC才能成为⊙O的切线.
二、选择题
1、 已知：某多边形的每个内角都是140°，则这个多边形是
A、正九边形 B、九边形 C、正十一边形 D、十一边形
2、
两圆内切，圆心距为3，一圆的半径为4，则另一圆的半径为
A、1 B、7 C、1或7 D、2
3、如图，正六边形两条平行边间的距离是1，则它的边长是
A、
B、
C、
D、
4、若两圆半径分别为R和r(R>r),圆心距为d,且R2+d2=r2+2Rd, 则两圆的位置关系为 A、内切 B、内切或外切
C、外切 D、相交
5、如图，一定滑轮的起重装置，滑轮半径为12cm，当重物上升4πcm时，滑轮的一条半径OA按逆时针方向旋转的度数为
A、12° B、30° C、60° D、90°
6、一个扇形半径30cm，圆心角120°，用它作一个圆锥的侧面，则圆锥底面半径为
A、5cm B、10cm C、20cm D、30cm
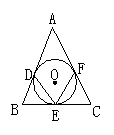
7、如图，△ABC的三边分别切⊙O于D，E，F，若∠A=50°，则∠DEF=
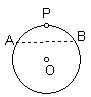A．65° B．50° C．130° D．80°
8、如图，⊙O为一张直径为6的圆形纸片，现将⊙O上的任意一点P与圆心O重合折叠后得折痕AB，则重叠部分图形的面积为
A、3π B、12π-
C、3π- D、
9、P为⊙O内一点，且OP=2 cm，过P的最长弦是6 cm，那么过P点的最短的弦等于
A、1 cm B、2 cm C、
cm D、2cm
10、如图，在⊙O中，直径AB⊥弦CD于点E，若EB＝1
，CD＝4，则
弦心距OE的长为 A、 1.5 B、 2 C、3 D、 4
三、解答题
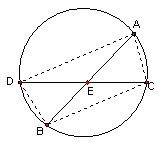1、AB、CD为⊙O内两条相交的弦，交点为E，且AB=CD。则以下结论中：①AE=EC、②AD=BC、③BE=EC、④AD∥BC，正确的有
。（写出所有正确的结论）（6分）试证明其中一个结论。（8分）
2、生活中的数学
中华民族的科学文化历史悠久、灿烂辉煌，我们的祖先几千年前就能在生产实践中运用数学.1300多年前，我国隋代建筑的赵州石拱桥的桥拱是圆弧形(如图9).经测量，桥拱下的水面距拱顶6 m时，水面宽34.64 m，已知桥拱跨度是37.4 m，运用你所学的知识计算出赵州桥的大致拱高.(运算时取37.4=14
，34.64=20
)
3、探究
已知：三角形ABC内接于⊙O，过点A作直线EF.
(1)如图1，AB为直径，要使得EF是⊙O的切线，只需保证∠CAE=∠_____，并证明之;
(2)如图2，AB为⊙O非直径的弦，(1)中你所添出的条件仍成立的话，EF还是⊙O的切线吗？若是，写出证明过程；若不是，请说明理由并与同学交流.
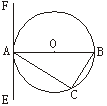
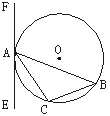
图1 图2