九年级数学中考模拟试卷
一、选择题（每小题3分， 共36分）
1、去年某市接待入境旅游者约876000人，这个数可以用科学记数法表示为（ ） A．
B.
C.
D.
2、在直角坐标系中，点M（1，2）关于y轴对称的点的坐标为（ ）
A．（1，-2） B.（2，-1） C.（-1，-2） D.（-1，2）
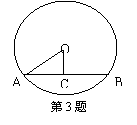
3、如右图，在⊙O 中,AB是弦，OC⊥AB，垂足为C，若AB=16，OC=6，
则⊙O的半径OA等于（ ）
A、16 B、12 C、10 D、8
4、下列图形中，是轴对称图形的为（ ）
 | |||
 | |||
Ａ Ｂ Ｃ Ｄ
5、在昆明“世博会”期间，为方便游客参观，铁道部门临时加开了南宁至昆明的直达列车．已知南宁至昆明的路程为828km，普快列车与直快列车由昆明到南宁时，直快列车平均速度是普快的1.5倍，若直快列车比普快列车晚出发2 h而先到4h，求两列车的平均速度分别是多少？设普快列车的速度为x km/h，则直快列车的速度为1．5xkm／h．依题意，所列方程正确的是（ ）
；
； 
6、在一个可以改变容积的密闭容器内，装有质量为m的某种气体，当
改变容积V时，气体的密度
也随之改变．与V在一定范围内满足
，它的图象如右图，则该气体的质量m为( )
A．1.4kg B．5kg
C．6.4kg D．7kg
7、从两副拿掉大、小王的扑克牌中，各抽取一张，两张牌都是红桃的
概率是（
）
A．
B． 
C．
D．
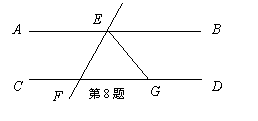
8、如图，AB∥CD ，直线EF分别交AB，CD于
E，F两点，∠BEF的平分线交CD于点G，若
∠EFG＝72°，则∠EGF等于( )
A． 36° B． 54° C． 72 ° D． 108°
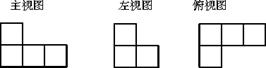9、右图是由一些相同的小正方体构
成的几何体的三视图，这些相同
的小正方体的个数是（ ）
A．4 B．5 C．6 D．7
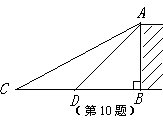10、如图为了测量某建筑物AB的高度，在平地上C处测得建筑物顶端A的仰角为30°，沿CB方向前进12m到达D处，在D处测得建筑物顶端A的仰角为45°，则建筑物AB的高度等于（ ）
A．6（
＋1）m B． 6 (—1) m
C． 12 (＋1) m D．12（－1）m
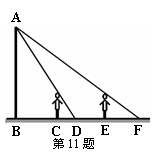
11、如右图，王华晚上由路灯A下的B处走到Ｃ处时，测得
影子CD的长为１米，继续往前走３米到达Ｅ处时，测
得影子EF的长为2米，已知王华的身高是1.5米，那么
路灯A的高度AB等于（ ）
Ａ．4.5米 Ｂ．6米
Ｃ．7.2米 Ｄ．8米
12、已知二次函数
与x轴交点的横坐标为
、
（
），则对于下列结论：①当x＝－2时，y＝1；②当
时，y＞0；③方程
有两个不相等的实数根、；④
，
；⑤
，其中正确的结论有( )．
A．2个 B．3个 C．4个 D．5个
二、填空题（每小题3分，共21分）
13、分解因式
=
．
14、圆锥的侧面展开图的面积为
，母线长为3，则该圆锥的底面半径为 ．
15、在函数y =
中，自变量x的取值范围是
.
16、一串有趣的图案按一定规律排列．请仔细观察，按此规律画出的第10个图案是 ；在前16个图案中 “ ”有________个．第2008个图案是
.
17、有一圆柱体高为10cm，底面圆的半径为4cm，AA1、BB1为相对
的两条母线，在AA1上有一个蜘蛛Q，QA=3cm，在BB1上有一只
苍蝇P，PB1=2cm，蜘蛛沿圆柱体侧面爬到P点吃苍蝇，
最短的路径是 cm。（Π取3.14，精确到0.1 cm）
18、有一张矩形纸片ABCD，其中AD=4cm，以AD为直径的半圆，
正好与对边BC相切，如图（甲），将它沿DE折叠，使A点落
在BC上，如图（乙），这时，半圆还露在外面的部分（阴影
部分）的面积是
．
 |
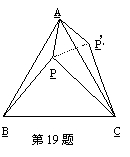
19、如图，设P是等边三角形ABC内的一点，PA=1，PB=2，PC=
，将△ABP绕
点A按逆时针方向旋转，使AB与AC重合，点P旋转到P´处，则
的值
是 （不取近似值）。
三、解答题（20、21、22题每题6分，23题7分、24题8分， 25、26题每题8分， 27题12分，共63分，其中26、27题题目附在答题卷上）
20、计算
－2sin45°－
－︱－3︱
21、先化简代数式，再求值： 
，其中
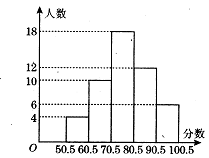22、某班同学进行数学测验，将所得成绩(得分取整数)
进行整理后分成五组，并绘制成频数分布直方图．
请结合直方图提供的信息，回答下列问题：
⑴ 该班共有多少名学生？
⑵请问 80．5～90．5这一分数段的频率是多少？
⑶ 这次成绩中的中位数落在哪个分数段内？
⑷ 这次测验的平均分的取值范围是多少？
23、近期，海峡两岸关系的气氛大为改善。大陆相关部门于2005年8月1日起对原产台湾地区的15种水果实施进口零关税措施，扩大了台湾水果在大陆的销售。某经销商销售了台湾水果凤梨，根据以往销售经验，每天的售价与销售量之间有如下关系：
| 每千克售价（元） | 50 | 49 | 48 | 47 | 46 | … |
| 每天销量（千克） | 40 | 42 | 44 | 46 | 48 | … |
设当单价从50元/千克下调了
元时，销售量为
千克；
（1）写出与间的函数关系式；
（2）如果凤梨的进价是20元/千克，当该经销商把售价定为多少元时，他能获得日最大利润？
（3）目前两岸还未直接通航，运输要绕行，需耗时一周（七天），凤梨最长的保存期为一个月（30天），若每天售价不低于30元/千克，问一次进货最多只能是多少千克？
24、某园林门票每张10元，只供一次使用，考虑到人们的不同需求，也为了吸引更多游客，该园林除保留原有的售票方法外，还推出一种“购个人年票”的售票方法（个人年票从购买之日起，可供持票者使用一年八年票分A、B、C三类；A类年票每张120元，持票者进人园林时无需再购买门票；B类年票每张60元，持票者进入园林时，需再购买门票，每次2元；C类年票每张40元，持票者进入该园林时，需再购买门票，每次3元．
⑴ 如果你只选择一种购买门票的方式，并且你计划在一年中用80元花在该园林的门票上，试通过计算，找出可使进人该园林的次数最多的购票方式；
⑵ 求一年中进人该园林至少超过多少次时，购买A类票比较合算．
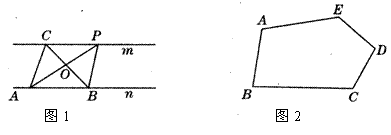
25、探究规律：如图1所示，已知：直线m∥n，A、B为直线n上两点，C、P为直线m上两点．
（1）请写出图1中，面积相等的各对三角形；
（2）如果A、B、C为三个定点，点P在m上移动，那么，无论P点移动到任何位置，总有________与△ABC的面积相等．理由是：_________________.
（3）解决问题：如图 2所示，五边形 ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图2所示的形状，但承包土地与开垦荒地的分界小路（图2中折线CDE）还保留着；张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多，右边的土地面积与开垦的荒地面积一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案（不计分界小路与直路的占地面积）．要求：写出设计方案，说明设计理由．并在图3画出相应的图形；
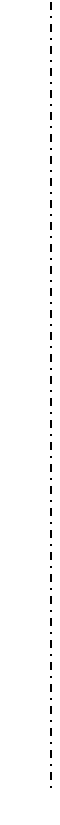九年级数学中考模拟试卷
一、选择题（每小题3分， 共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每小题3分， 共21分）
13、 ；14、 ；15、 ；
16、 、 、 ；
17、 ；18、 ；19、 。
三、解答题（20、21、22题每题6分，23题7分、24题8分， 25、26题每题8分， 27题12分，共63分，其中26、27题题目附在答题卷上）
20、
21、
22、
23、
24、
25、（1） ；
（2） ， ；
（3）方案设计及理由：
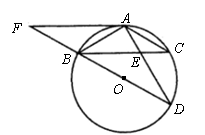
26、如图，
为⊙
的直径，
，
交
于
，
，
．
（1）求证：
，并求
的长；
（2）延长
到
，使
，连接
，那么直线与⊙相切吗？为什么？
 |
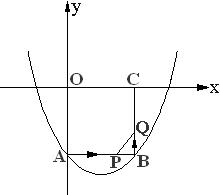
27、如图所示, 在平面直角坐标系xOy中, 正方形OABC的边长为2cm, 点A、C分别在y
轴的负半轴和x轴的正半轴上, 抛物线y=ax2+bx+c经过点A、B, 且12a+5c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以2cm/s的速度向点B移动, 同时点Q由点B开始沿BC边以1cm/s的速度向点C移动.
①移动开始后第t秒时, 设S=PQ2(cm2), 试写出S与t之间的函数关系式, 并写出t的取值范围;
②当S取得最小值时, 在抛物线上是否存在点R, 使得以P、B、Q、R为顶点的四边形是平行四边形? 如果存在, 求出R点的坐标, 如果不存在, 请说明理由.
2006学年九年级数学中考模拟试卷
一、选择题（每小题3分， 共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | C | D | C | D | D | B | B | A | B | B |
二、填空题（每小题3分， 共21分）
13、 7x（x+3）（x-3） ；14、 2 ；15、 x≥-2且x≠3 ；
16、 画正的脸 、 5 、 画正的脸 ；
17、
13.5
；18、 
；19、
。
三、解答题（20、21、22题每题6分，23题7分、24题8分， 25、26题每题8分， 27题12分，共63分，其中26、27题题目附在答题卷上）
20、解：原式=
………………………………4分
=-7 ………………………………6分
21、解：原式=
………………………3分
当时,原式=
…………6分
22、解(1)50人；…1分(2) 
；…2分 (3)70.5到80.5分数段；…3分
(4) 
≤x≤
……………4分
72.2≤x≤81.2
答：略 …………6分
23、解：（1）
…………………………………………2分
（2）销售价定位30元/千克时，令日利润为W元
W=（50-20-x）（40+2x）
=-2x2+20x+1200 ………………………4分
当x=
时W取最大值。此时此时售价为50-5=45元 …5分
答：略 ……………………………6分
3）设一次进货最多
千克
……………………………………………………7分
∴一次进货最多不能超过1840千克。 ………………………8分
24、
25、（1） △ABC和△ABP、△AOC和△ BOP、△CPA和△CPB ； ………3分
（2） △ABP ， 因为平行线间的距离相等，所以无论点P在m上移动到任何位置，总有△ABP与△ABC同底等高，因此，它们的面积总相等． ； …5分
（3）方案设计及理由：
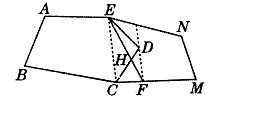连接EC，过点D作DF∥EC，交CM于点F，连接EF，
EF即为所求直路位置．
设EF交CD于点H，由上面得到的结论可知：
SΔECF=SΔECD，SΔHCF=SΔEDH，所以S五边形ABCDE=
S五边形ABCFE，S五边形EDCMN=S四边形EFMN．
方案设计及理由得2分，作图得2分。
26、（1）证明：
，
．
又
，
．
………………………3分
．
．
．
……………………………………5分
（2）直线与
相切．
……………………………………6分
连接
．
为的直径，
．
．
．
，
．
．
直线与相切．
…………………9分
27. 解: (1)据题意知: A(0, －2), B(2, －2)
∵A点在抛物线上, ∴C=－2
∵12a+5c=0, ∴a=
由AB=2知抛物线的对称轴为: x=1
即: 
∴抛物线的解析式为: 
……………………3分
(2)①由图象知: PB=2－2t, BQ= t
∴S=PQ2=PB2+BQ2=(2－2t)2 + t2
即 S=5t2－8t+4 (0≤t≤1) ……………………………………5分
②∵S=5t2－8t+4 (0≤t≤1)
∴S=5(t
)2 +
(0≤t≤1)
∴当t=时, S取得最小值. …………………………………6分
假设存在点R, 可构成以P、B、R、Q为顶点的平行四边形.
这时PB=2
=0.4, BQ=0.8, P(1.6,
－2), Q(2, －1.2)
………7分
a、过Q作QR∥BP交抛物线于R。
当y=-1.2时，x1=2.4，x2=-0.4
∴R1（2.4,-1.2）,R2（-0.4,-1.2）
∴QR1=0.4, QR1=2.4
∵BP=0.4
∴QR1=BP, QR2≠BP
此时有QR1
PB,则四边形BPQR为平行四边形.
∴R的坐标为(2.4, －1.2) …………………………9分
b、过P作PR∥BQ交抛物线于R。
当x=1.6时,y=-2.4
∴R（1.6,-2.4）
∴PR=0.4
∵BQ=0.4
∴PR=BQ
此时有PR BQ,则四边形BQPR为平行四边形.
∴R的坐标为（1.6,-2.4） …………………………11分
c、过B作BR∥PQ交抛物线于R。
直线PQ:y=2x-5.2
直线BR:y=2x-6
则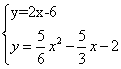
解得x1=2，x2=2.4
∴另一交点为（2.4,-1.2）
此时QR≠PB
则四边形BQPR不是平行四边形. …………………………12分