九年级数学周练试卷姓名
一、选择题（满分36分）
每题只有一个正确答案，请把各题的正确答案分别填在下表中：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1. 有资料表明：被称为“地球之肺”的森林正以每年公顷的速度从地球上消失，每年森林消失量用科学计数法可表示为（ ）公顷。
(A)
(B)
(C)
(D)
2．甲、乙、丙三种果冻的单价分别为5元、7元、8 元，如果混合出售，定价为6元，则应按（ ）比例配比才不会亏损
（A）3：2：1 （B）3：1：1 （C）4：3：2 （D）5：2：2
3．下列每张方格纸上都画有一个圆，只用不带刻度的直尺经过一次操作就能确定圆心位置的是
 |
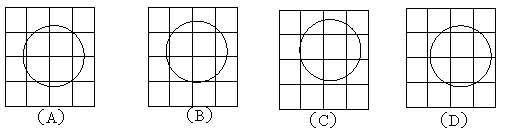4．在下列八个汉字中：“天、目、中、上、下、土、田、显”，是轴对称图形的有（ ）。
(A)5个 (B)6个 (C)7个 (D)8个
5．已知线段AB，以A、B为顶点画位置不同的正方形，一共可以画（ ）
(A)1个 (B)2个 (C)3个 (D)4个
6．在①不在一直线上三点确定一个圆；②平分弦的直径垂直于弦；③三角形的内心到各边的距离相等；④圆的两条不是直径的相交弦不能互相平分.
其中正确的命题的个数是
（A）1 （B）2 （C）3 （D）4
7．某手表每小时比准确时间慢3分钟上，若在清晨4点30分时与准确时间对准，则当天上午该手表指示时间是10点50分时，准确时间应该是
（A）11点10分 （B）11点9分（C）11点8分（D）11点7分
8．电脑福利彩票中有两种方式“22选5”“29选7”，若选中号码全部正确则获一等奖你认为获一等奖机会大的是
（A）“22选5” （B）“29选7”（C）一样大（D）不能确定
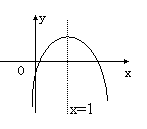
9．函数y=ax2+bx+c(a<0)的图象如右图所示,则 ①c<0;
②b>0; ③4a+2b+c>0; ④(a+c)2<b2,
其中正确的有
（A）1个 （B）2个 （C）3个 （D）4个
10．某原料供应商对购买其原料的顾客实行如下优惠办法：
（1） 一次购买金额不超过1万元，不予优惠；
（2） 一次购买金额超过1万元，但不超过3万元，给九折优惠；
（3） 一次购买超过3万元的，其中3万元九折优惠，超过3万元的部分八折
优惠．某厂因库容原因，第一次在该供应商处购买原料付款7800元，第二次购买付款26100元，如果他是一次购买同样数量的原料，可少付金额为（ ）．
（A）1460元 （B）1540元 （C）1560元 （D）2000元
11．下列命题：
①检查一个人的的血型需抽取血样，这时的总体和样本都是指一个人的血型；
②已知α2+α-1=0，β2+β-1=0，且α≠β，则αβ+α+β=0
③若直角三角形的两边是3和4，则第三边是5；
④若半径分别是1和3的两圆相交，则公共弦的最大值是2
⑤李小明同学用一个半径为3cm,圆心角为1200的扇形铁皮做一个圆锥形模型的侧面，则这个圆锥底面圆的直径为2cm
⑥小宁买了20个练习本，店主给他八折（即标价的80%），优惠，结果便宜了1．60元，则每个练习本的标价是0．20元
其中正确命题的个数是
(A)4个 (B)3个 (C)2个 (D)1个
12．一辆客车，一辆货车和一辆小轿车在同一条路上，各自的速度不变，向同一目标地行驶，在某一时刻，货车在中，客车在前，小轿车在后，且货车与客车、小轿车之间路程相等。走了10分钟小轿车追上了货车；又走了5分钟，小轿车追上了客车，问再过（ ）分钟，货车追上了客车。
（A）5 （B）10 （C）15 （D）30
二．填空：（每题3分，共24分）
13、若a<0,点(a,b)、(a-1,c)均在双曲线
上，则b c(填“>”、“<”或“=”)
14、观察下面一列有规律的数
， 根据这个规律可知第n个数是
（n是正整数）
15、抛物线C1的解析式是
，抛物线C2与抛物
线C1关于x轴对称，则物线C2的解析式： ；
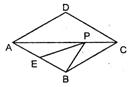16．菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P
是对角线AC上的一个动点，则PE+PB的最小值是 ．
17、在某报《自测健康状况》的报道中，自测血液结果与相应的年龄的统计数据如下表，观察表中数据的特点，用适当的数填入表中的空格中。
| 年龄（岁） | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 |
| 收缩压（水银柱 毫米） | 110 | 115 | 120 | 125 | 130 | 135 | 140 | |
| 舒张压（水银柱 毫米） | 70 | 73 | 75 | 78 | 80 | 83 | 88 |
18．右图是用8个大小一样边长为整数的矩形搭成的,其中中间阴影部分是
一边长为2的正方形,试写出符合要求的三个不同的矩形边长_______．
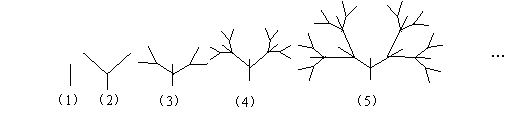
19．下面是按照一定规律画出的一列“树型”图：经观察可以发现：
图（2）比图⑴多出2个“树枝”，图⑶比图⑵多出5个“树枝”，图
⑷比图⑶多出10个“树枝”，照此规律，图⑺比图⑹多出_________
个“树枝”．
 |
20．观察图形，若第一个图形阴影部分的面积为1，则第n个图形阴影部分面
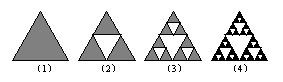积为
三、解答题(本大题共10小题,第21-27题每题8分)
21． 先化简，再计算
，其中
＝3.
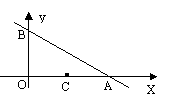
22．如图，已知点A与点B的坐标分别为（4，0），（0，2）（1）求直线AB的解析式；（2）过点C（2，0）的直线（与x轴不重合）与△AOB的另一边相交于点P，若截得的三角形与△AOB相似，求点P的坐标。
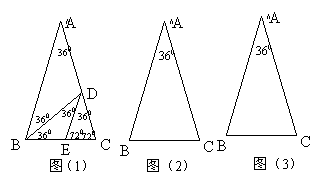23.仿照图（1），请你再设计两种不同的分法，将△ABC分割成3个三角形，使得每个三角形都是等腰三角形，（图（2）、图（3）供画图用，作图工具不限，不要求写出画法，不要求证明；要求标出所分得的每个等腰三角形三个内角的度数）
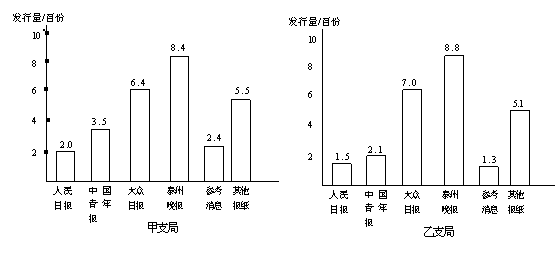24.我市城镇邮政局对甲、乙两个支局的报刊发行部2004年度报纸的发行量进行了统计，并绘成统计图如下：
请根据上面统计图反映的信息，回答问题：
⑴哪个支局发行《泰州晚报》的份数多？多多少？
⑵分别写出上面两个统计图中提供的6个统计数据的中位数；
⑶已知甲、乙两个支局所服务的居民区住户分别是11280户、8600户，哪个居民区平均每户订阅报纸的份数多？试说明理由。
25.同时抛掷两枚硬币，按照正面出现的次数，可以分为“2个正面”、“1？?个正面”和“没有正面”这3种可能的结果，小红与小明两人共做了6组实验，每组实验都为同时抛掷两枚硬币10次，下表为实验记录的统计表：
| 结果 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
| 两个正面 | 3 | 3 | 5 | 1 | 4 | 2 |
| 一个正面 | 6 | 5 | 5 | 5 | 5 | 7 |
| 没有正面 | 1 | 2 | 0 | 4 | 1 | 1 |
（1） 由上表结果，计算出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是多少？
（2） 从他的实验记录和你自己的生活经验中，你能否对这三种结果的可能性的大小作出预测？并通过树状图进行验证。
（3） 小红与小明约定：只抛一枚硬币，掷出正面小红得1分，掷出反面小明得1分，先得100分的人赢得一个大蛋糕，但因小红有事，游戏中途停止，此时小红得了99分，小明得了98分，问蛋糕应如何分配？
26.（本题满分8分）
泰州市溱湖风景区，为了吸引更多的游客，特推出集体购票优惠票价的办法，其门票价目如下表：
| 购票人数 | 1至50人 | 51至100人 | 101人以上 |
| 每人门票价 | 6元 | 5元 | 4元 |
某校初二（1）、（2）两班共104人（其中二（1）班人数多于二（2）班人数）准备在暑假期间去溱湖旅游．若两班都以班为单位购票，一共要支付570元．
(1) 如果两班联合起来，作为一个团体购票，那么比以班为单位购票可以节约多少钱？ (2) 试问两班各有多少名学生？ (3) 如果初二（1）班有10人因特殊情况不能前往旅游，那么又该如何购票才能最省钱？
27.（本题10分）
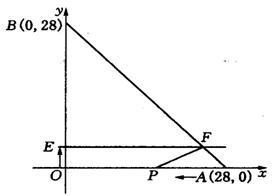如图所示，已知A、B两点的坐标分别为（28，0）和（0，28），动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动．动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动（即EF∥x轴），并且分别与y轴、线段AB交于E、F点．连结EP，设动点P与动直线EF同时出发，运动时间为t秒．
（1）当t＝1秒时，求梯形OPFE的面积．t为何值时，梯形OPFE的面积最大，最大面积是多少？
（2）当梯形OPFE的面积等于三角形APF的面积时．求线段PF的长；
（3）设t的值分别取t1、t2时（t1≠t2），所对应的三角形分别为△AF1P1和△AF2P2．试判断这两个三角形是否相似，请证明你的判断．
28.（本题12分）
如图，在直角坐标系xoy中，半径为2的⊙O与x轴交于A、B两点，与y轴交于点P，T是OB上一点，OT=a（0＜a＜2），过A作AC⊥AB，且AC=AT，连结CP并延长交半圆于另一点Q，且Q恰为弧PB的中点
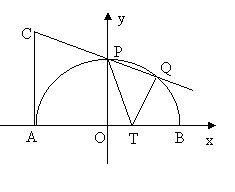（1）求出点Q的坐标
（2）求直线CP的解析式及a的值；
(3)由点P发出的光线，经过T点处反射后，反射光线是否通过点Q？请说明理由.
29.（本题12分）
已知：如图，平行四边形ABCD的边BC在x轴上，点A在y轴的正方向上，对角线BD交y轴于点E，AB＝
，AD＝2，AE＝
．
（1）求点B的坐标；
（2）求过A、B、D三点的抛物线的解析式；
（3）（2）中所求的抛物线上是否存在一点P，使得
＝
？若存在，请求出该点坐标；若不存在，请说明理由。
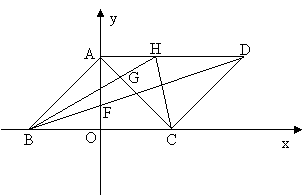（4）若点H在线段AD上，BH交AC于点G，且BH=BC，求tan∠ACH.