九年级数学综合考试题（一）

九年级数学综合考试题（一）

时间：120分钟　　　满分：120分

题号	一	二	三	四	五	六	总分
分数

一、选择题：（每小题3分，共36分）

1、二次函数 y=2x²﹣4x的图象与x轴的两个交点坐标为（　　）

A、（0，0），（0，2）　　　　　　 B、（0，0），（2，0）　　　　　　　　　　　　　　　　 

C、（0，0），（0，-2）　　　　　　 D、（0，0）,（-2，0）

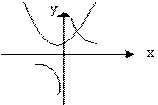
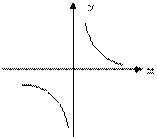
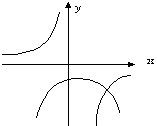
2、　　　　　　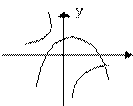  函数y=ax² -a与y=　(a≠0)在同一直角坐标系中的图象可能是（　　）。

　　　　　　　　　　　　　　　　　　

　　　(A)　　　　　　　　　　　　　　 (B)

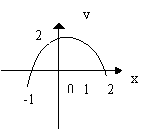
　　　　　 (C)　　　　　　　　　　　　　  (D)

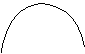
3、　　　　　　  如图3－1中，抛物线的函数表达式是（　  ）。

图3－1

A、y=x²-x+2　　　　  B、y=-x²-x+2

C、　　　　　  y=x²+x+2　　　　 D、y= -x²+x+2　 　　　　　 

4、　　　无论x为何值，y =ax² +bx+c恒为正的条件（　　）。　

A、a﹤0，b² -4ac﹤0　　　　 B、a﹤0，b² -4ac﹥0

C、a﹥0　b² -4ac﹤0　　　　D、a﹥0， b² -4ac﹥0

5、　　　把抛物线y= x² +bx+c的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式是y=x²-3x+5，则有（　　）。

 A、b=3，c=7　　　　　　　 　B、b=－9，c=－15

 C、b=3，c=3　 　　　　　　　D、b=－9，c=21

6、　　　图6－1中是由一些相同的小正方形叠成的几何体的三种视图，则这个几何体中小正方体的个数是（　　）。

　　　　主视图　　　　　　　　　　　　 左视图　　　　　　　  俯视图

　　　　　　　　　　　　　　　　 图6－1

A、7　　　　  B、6　　　　  C、5　　　　　  D、4

7、　　　　　　  ΔABC和ΔDEF相似且相似比为，那么ΔDEF和ΔABC的相似比为（　  ）。

A、　　　 B、　　　　 C、　　　　　D、

 8.在Rt ΔABC中，∠c＝90°，AC＝7cm，BC＝24cm，则 sinA 为（　　）。

A、　　　 B、 　　　　 C、　　　　 D、

9、　　　　　　  图9－1是某个物体的三视图，则该物体是（　　）。sinA

 

 

俯视图　　　　左视图　　　　　　　 主视图　（图　9－1)

A、 圆柱　　 B、圆台　　C、圆锥　　 D、球

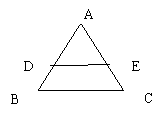10、图10－1中，在ΔABC中，DE//BC,BC=6cm,且SΔADE : SΔABC＝1:4那么DE为（　　）。　　　　　　　　　　　　　　　　

A、　　　　　   2 cm　 B、4 cm　C、 3 cm　D、2cm

　　　　　　　　　　　　　　　　　　　　　　　　　 图（10－1）

11、如图11－1中，小明站在C处看甲、乙两楼楼顶上的点A和点E，点C、E、A三点在同一条直线上，点D、B分别在点E、A的正下方，且D、B、C三点在同一条直线上，B、C两点相距20m，D、C两点相距40m,乙楼高BE为15m,甲楼AD高为（　　）。　 (小明身高不计）

A、40　　  B、15

C、20　　　D、30

　　　　　　　　　　　　　　

(图11－1）

12、在比例尺为1: 2000的地图上，面积为25Cm^­2的基地，实际面积是（　　 ）Cm²　。

A、　　　　　  5× 10⁴　 B、0.5× 10⁸　　C、1×10⁸　D、10×10^8.

二、　　　　 填空题：（每小题3分，共24分）

13、抛物线y=－3（x-1）²－3的顶点坐标是　　　　  ，对称轴 是　　　　 。

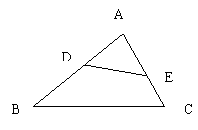14、如图14－1中，DE分别是ΔABC的边AB、AC上的点，请你添加一个条件，使ΔADE～ΔABC，你添加的条件是　　　　　　　  。

　　　　　　

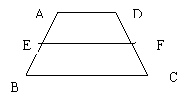　　　　　　　  图15-1　　　　　　　　　　　  图14-1　　　　　　　　　　　　　　　　　　 

15、如图15－1中，梯形ABCD中 ，AD//BC，AD＝2，BC＝6，EF是中位线，那么S_梯AEFD : S_梯ABCD=（　　）。　　　　　　　　　　　　　　　   

16、已知3tanA-=0,求∠A=　　　　。

17、已知m=tan30°· tan60°,则m= 　　　　 。　　　

18、Sin57°=cos　　　 °;　　cos68°=Sin　　　 °。

19、二次函数y=2x²,　y= -2x² ,　 y=　x²的图象的共同点是⑴　　　　　　　　 

 　　　　　　　 ⑵　　　　　　　　　　   ⑶　　　　　　　　 。

20、若∠α为锐角，且tanα是方程x²-2x-3＝0的一个根，则Sinα＝ 　　。

三、　　　　 作图题：（6分）

21、如图，在直角坐标系中，作出以A（2，6）、B（4，2）、C（6，2）、

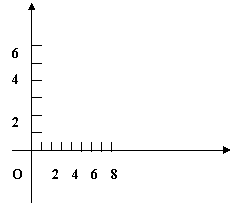
D（6，4）为顶点的四边形ABCD的位似图形，使新四边形与原四边形对应边的比为1: 2，位似中心为原点。

四．解答题：（共26分，22、23各8分，24题10分）

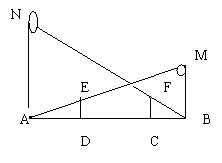22、如图22－1所示，小明在晚上由路灯A走向路灯B，当他行到D时发现，他在路灯B下的影子长为2m，接着他又走了6.5m到C处，此时在灯AF的影子顶端正好落在B点，已知小明身高为1.8m处，路灯B高9m。

（1）　　 计算小明在C处路灯A下的影长。

（2）　　 计算路灯A的高度。

23.如图表23_1所示抛物线 y=-x²+5X+n经过点A(1 ,0)与y轴交于点B.

(1)求抛物线的解析式．

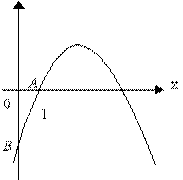(2)若点P是Y轴正半轴上一点，且ΔPAB是以AB为腰的等腰三角形，试求点P的坐标。　　　　　　　　 

　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　

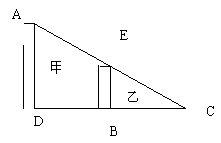
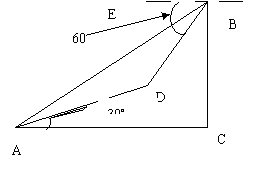24. 某校九年级（3）斑的一个学习小组进行测量小山高度的实践活动，部分学生在山脚点A测得山腰上一点D的仰角为30° ,并测得AD的长度为180米,另一部分同学在山顶点B测得山脚点A的俯角为45°即∠EBA=45°、山腰点D的俯角为60°即∠EBD=60°,请你帮他们计算出小山的高度BC.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　°　　　　　　 

　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

五 .证明题:(每小题8分,共16分)

25.已知ΔABC,点D,E分别在边AB,AC上,连接DE并延长交BC的延长线于点F,连接DC,BE,若∠BDE+∠BCE=180度.

(1)写出图中三对相似三角形,(不添加字母和线)

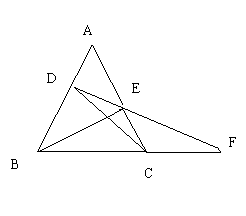(2)请你在所找出的相似三角形中选出一对,并说明相似的理由.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

26.在⊙O中,弦AB与CD相交于点P,连接AC,DB.

(1) 求证:PA·PB=PC·PD

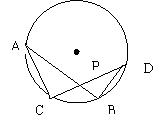(2) 当AC : DB为何值时, S_ΔPAC : S_ΔPDB = 4

六.应用题:(共12分)

某产品每件成本10元,试销售阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:

X（元）	1 5	20	30	…
Y（件）	25	20	10	…

若日销售量y是销售价x的一次函数.

(1)求出日销售量y(件)与销售价x(元)的函数关系式.

(2)使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?