九年级一模数学试卷

考生注意：

本卷共八大题，计 28 小题，满分 120 分，考试时间 120 分钟。

一、选择题（每小题2分，共24分）

1．若a的绝对值为２，则的a值为---------------------（　　）

Ａ．２　　　　Ｂ．－２　　　　Ｃ．２　　　Ｄ．

２．某天中午南京市的气温是１℃，到傍晚下降了３℃，那么傍晚的气温是------（　　）

Ａ．４℃　　　Ｂ．２℃　　　Ｃ．－２℃　　　Ｄ．－３℃

3．海南的富铁矿是国内少有的富铁矿之一，储量居全国第６位，其储量约为吨,用科学记数法表示应为----------　　　 ------------- (　 )

Ａ．237×10　　B．2.37×10　 C．2.37×10　 D．0.237×10　

4．下列各式计算结果中正确的是--------------------（　　）

Ａ．a+a=a　　 B．(3a)=6 a　　C．(a+1)=a+1　　D．a•a=a

5．两圆的半径分别为2㎝和3㎝, 它们的圆心距为5㎝, 则这两圆的位置

关系是--------------------------------- (　　)

Ａ．相离　　　　 B．外切　　　　C．相交　　　　 D．内切

6．面积是15cm的正方形，它的边长的大小在------------------------------------------（　　）

Ａ．１cm与２cm之间　　　　　 B．２cm与３cm之间　　

　　　C．３cm与４cm之间　　　　　　 D．４cm与５cm之间　

7．为筹备班级的初中毕业联欢会, 班长对全班学生爱吃哪几种水果作了民意调查, 那么最终买什么水果, 下面的调查数据中最值得关注的是------------------------------ (　　)

Ａ．中位数　　　 B．平均数　　　C．众数　　　　 D．加权平均数

8．在一个暗箱里放入除颜色外其它都相同的３个红球和11个黄球,搅拌均匀后随机任取一个球,取到红球的概率是------------------- (　　 )

Ａ．　　　　 B．　　　　 C．　　　　　 D．

9．用配方法将y=—x²+2x+3化为ｙ=a(x－h)²+k的形式，正确的是----(　　)

Ａ．ｙ=－(x－１)²+４　　　　　　　　B．ｙ=－(x－１)²+２

C．ｙ=－(x＋１)²+４　　　　　　　　 D．ｙ=－(x＋１)²+２

10．一个形状圆锥的冰淇淋无底纸筒，其底面直径为６㎝，母线长为５㎝，

围成这样的冰淇淋纸筒所需纸片的面积是--------------------（　　）

Ａ．66㎝　　B．30㎝　　 C．286㎝　　D．15㎝　

11．如图, 是由几个小正方体所搭成的几何体的俯视图, 小正方形中的数字表示在该位置的小正方体的个数, 这个几何体的主视图是-------------------------------------- (　　 )

C

12．如图，在平面直角坐标系中，圆心在x轴的⊙O′与两坐标轴分别交于A、B、C、D四点，已知A(-1，0)，B(9，0)，则线段CD的长度为（　　）　

A. 3　　 B．4　　　C．6　　 D. 8

二、填空题(每小题3分,共12分)

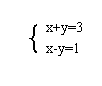
13．方程组组　　　　　　　的解为　　　 .

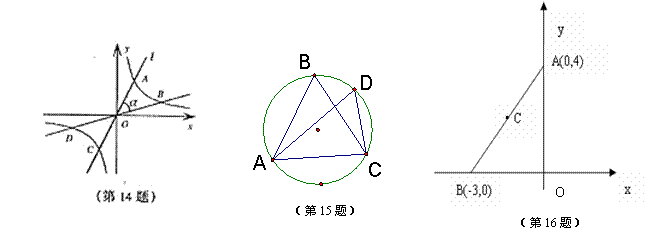
14．如图，直线L与双曲线交于A、C两点，将直线l绕点O顺时针旋转度角，与双曲线交于B、D两点，则四边形ABCD的形状一定是_____________形。

15．如图4，在⊙O中，∠ACB＝∠D＝60°，AC＝3，则△ABC的周长为_________。

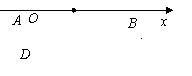
16．如图，在直角坐标系中有两点A（0,4）和B(-3,0),点C是AB的中点,如果点D在X轴上,若以B、C、D三点为顶点的三角形与以A、B、O三点为顶点的三角形相似，则D的坐标是　　　　　　．

三、(第17题5分，第18、19每题6分，第20题7分，共24分)

17．计算：

18．先化简，再求值：，其中．

19．求不等式组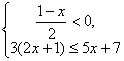的整数解．

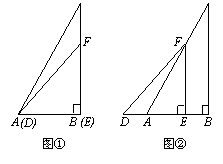
20．在△ABC中，∠BAC=90°，延长 BA 到D，使AD=AB，点E、F分别为边BC、AC的中点．

（1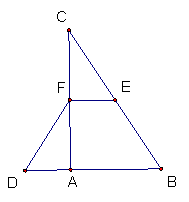）　　　求证：DF=BE

（2）若CF=2．CE=.求tan∠ADF

四、(第21、22题每题6分，第23题7分，共19分，)

21．A城市每立方米水的水费是B城市的1.25倍，同样交水费20元，在B城市比在A城市可多用2立方米水，那么A、B两城市每立方米水的水费各是多少元？

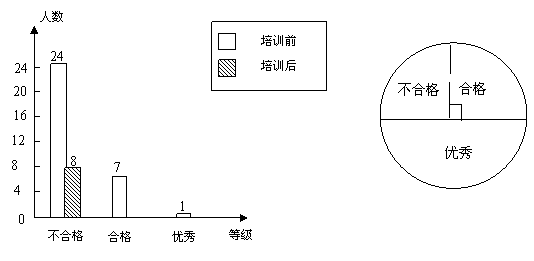
22．某校320名学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级。为了了解电脑培训的效果，随机抽取其中32名学生两次考试考分的等级，并将培训前后学生两次考试考分的等级用条形统计图（不完整）和培训后学生考试考分的等级用扇形统计图表示如下，试回答下列问题：

（1）这32名学生经过培训，考分等级“不及格”的百分比由______下降到__________；

（2）补全题中培训后学生考分等级的条形统计图；

（3）估计该校320名学生，培训后考分等级为“合格”与“优秀”的学生共有_______名；

23．桌面上放有4张除数字外完全相同的卡片，正面分别标有数字1，2，3，4，把这些卡片反面朝上洗匀后放在桌面上，甲从中任意抽出一张，记下卡片上的数字后仍反面朝上放回桌面洗匀，乙从中任意抽出一张，记下卡片上的数字，然后将这两数相加；

（1）请用列表或画树状图的方法求两数和为5的概率；

（2）若甲与乙按上述方式作游戏，当两数之和为5时，甲胜；反之则乙胜；若甲胜一次得12分，那么乙胜一次得多少分，这个游戏对双方才公平。

五、(第24题8分，第25题7分，共15分)

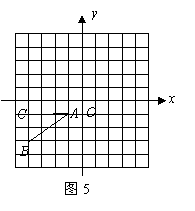
24．如图，已知的顶点的坐标分别是．
（1）（i）作出关于原点中心对称的图形到；

（ii）画出将绕原点按顺时针方向旋转后得到　　　的图形△A₂B₂C₂．

（2）（i）填空：点A₂的坐标为　　　　；

（ii）选择：不可能由△A₂B₂C₂按下列的哪种方式得到（　　）

A．平移　　　　 B．旋转　　　　C ．先平移后旋转　　　D．先旋转后平移

25．如图，两块三角板，其中∠B＝∠E＝90°,∠C＝30°,∠FDE＝45°AB＝DE＝

。先将两块三角板叠合在一起，使边DE与AB重合(如图①)，再将△DEF沿AB所在直线向左平移，使点F落在AC上(如图②)，求平移距离BE的长；

六、(第26题8分，第27题9分，共17分)

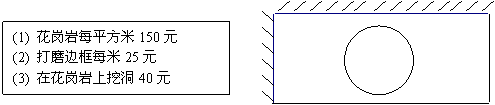
26、张老师家装修，想做一块长比宽多1米的长方形的花岗岩台面板，他来到做花岗岩面板的商店，看到制作费用表：张老师考虑到面板有两边靠墙，如图所示，台面只需打磨两边,且在花岗岩面板上需挖一个洞安装水池。张老师制作这一台板的一共花了265元，求这块台板的长与宽　

墙

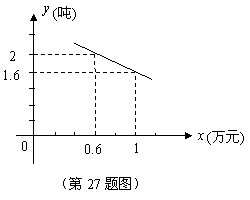
27．北方某水果商店从南方购进一种水果，其进货成本是每吨0.4万元，根据市场调查这种水果在北方市场上的销售量（吨）与每吨的销售价（万元）之间的函数关系如下图所示：

（1）求出销售量与每吨销售价之间的函数关系式；

（2）如果销售利润为（万元），请写出与之间的函数关系式；

（3）当每吨销售价为多少万元时，销售利润最大？最大利润是多少？

七、(本题9分)

28．如图，矩形ABCD中，AD=3cm,AB=2cm，点E沿A→D方向移动，点F沿D→A方向移动，速度都是1cm/s。如果E、F两点同时移动，且当E、F两点相遇即停止．设移动时间是t(s)．

(1)　　　当BE与CF所在直线的夹角是60°时，t是多少？

(2)　　　当四边形BCFE的对角线BF与CE的夹角是90°时，t是多少？

(3)　　　当△ABE的外接圆与△CDF的外接圆外切时，t是多少？