九年级数学阶段性测试卷(问卷)
( 试卷总分:120分 考试时间:100分钟 2006.12)
一、选择题:(下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内。)
1. 计算![]() 结果是( )
结果是( )
A.-![]() B.
B.![]() C.-3ax D.-
C.-3ax D.-![]()
2.下列命题中,真命题是( )
A.两条对角线相等的四边形是矩形 B.两条对角线垂直的四边形是菱形
C.两条对角线垂直且相等的四边形是正方形; D.两条对角线相等的平行四边形是矩形
3. 气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )
A.本市明天将有80%的地区降水 B.本市明天将有80%的时间降水
C.明天肯定下雨 D.明天降水的可能性比较大
4.关于x的方程![]() x2=x+
x2=x+![]() ,小明作出如下判断,正确的有( )
,小明作出如下判断,正确的有( )
① 它一定是一元二次方程; ② 它的一次项系数是1,③ 这个方程一定有实数根
A. 0个 B. 1个 C. 2个 D. 3个
5.下列说法错误的是 ( )
A.顶角和腰对应相等的两个等腰三角形全等 B.顶角和底边对应相等的两个等腰三角形全等
C.斜边对应相等的两个等腰直角三角形全等 D.两个等边三角形全等
6.把抛物线向下平移3个单位,向左平移2个单位后得到抛物线y=2x2-4x+3
则原来抛物线的函数关系式是( )
A. y=2(x+1)2+4 B, y=2(x+1)2+5 C. y=2(x-3)2+4 D y=2(x-3)2+5
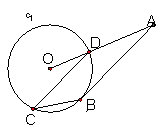 7.如图AB切⊙O于B,AO交⊙O于D,C是圆上一点,∠DCB=300.
7.如图AB切⊙O于B,AO交⊙O于D,C是圆上一点,∠DCB=300.
|
8.如图,已知正方形ABCD,P、Q分别是BC、CD上的点,M、N分别是AP、PQ的中点,
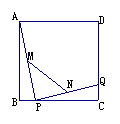 当点P、Q分别在BC、CD上以相同的速度同时从B、C出发向C、D运动时,那么下列结论
当点P、Q分别在BC、CD上以相同的速度同时从B、C出发向C、D运动时,那么下列结论
成立的是( )
(A)线段MN的长逐渐增大 (B)线段MN的长逐渐减小
(C)线段MN的长不变 (D)线段MN长的变化没有规律
|
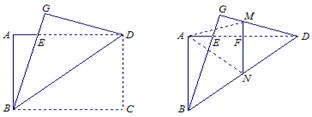 10.在矩形ABCD 中,AB=3, AD=4,将其沿对角线BD折叠,顶点C的对应位置为G(如图1),BG交AD于E;再折叠,使点D落在点A处,折痕MN交AD于F,交DG于M,交BD于N,展开后得图2,则折痕MN的长为( ).
10.在矩形ABCD 中,AB=3, AD=4,将其沿对角线BD折叠,顶点C的对应位置为G(如图1),BG交AD于E;再折叠,使点D落在点A处,折痕MN交AD于F,交DG于M,交BD于N,展开后得图2,则折痕MN的长为( ).
A. ![]() B.
B. ![]()
|
|
二、填空题:(请把最后结果填在答题卷中相应的横线内,每小题写4分,共24分)
11、实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0. m,则这个数用科学记数法表示
12、某公司计划用两年时间实现产品的销售总量翻一翻,设每年增长的百分率为x,则可列方程______
 13、用反证法证明“已知⊿ABC,求证∠A, ∠B, ∠C中至少有两个角是
13、用反证法证明“已知⊿ABC,求证∠A, ∠B, ∠C中至少有两个角是
锐角”时,应假设_______________.
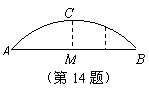
 14
如图,一桥拱呈抛物线状,桥的最大高度是8米,跨度
14
如图,一桥拱呈抛物线状,桥的最大高度是8米,跨度
是20米,在线段AB上离中心M处5米的地方,桥的高度是 m.
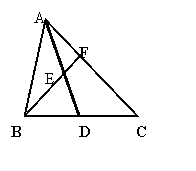
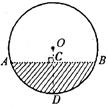
|
AB=![]() ,以点D为圆心作⊙D,若A,B,C三点至少有一点在圆内,
,以点D为圆心作⊙D,若A,B,C三点至少有一点在圆内,
至少有一点在圆外,则⊙D的半径![]() 满足____________.
满足____________.
16、⊿ABC中,D是BC中点,E是AD中点,BE交AC于F.一只蚂蚁
|
三、解答题:(解答应写出文字说明,证明过程或推演步骤,写在答题卷中相应的位置上)
17. 解下列方程(1)![]() (2)
(2)![]()
18
计算(1) ![]() (2)
(2) ![]() .
.
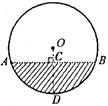
 19如图,水平放置的一个油管的截面半径为13cm,其中有油部分
19如图,水平放置的一个油管的截面半径为13cm,其中有油部分
油面宽AB为24cm,求截面上有油部分的面积(单位:cm)
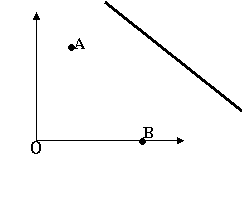
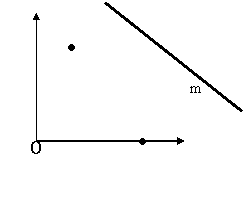 20.如图,点O是直角坐标系的原点,表示工地,
20.如图,点O是直角坐标系的原点,表示工地,
|
直线m表示公路.现在准备从公路运送建材到工
地,汽车发出的噪音影响的半径是450,请你通过
|
下从两个小区之间通过.(单位都是米)
21.某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示. 根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如下图所示,每得一票记作1分.
(1)根据实际需要,单位将笔试、面试、民主评议三项测试得分按![]() 的比例,确定个人成绩,那么谁将被录用
的比例,确定个人成绩,那么谁将被录用
 (2)若上述三项的比例都是整数,且它们的和是10,求乙的得分是780分的情况下, 上述三项的比例的可能的值
(2)若上述三项的比例都是整数,且它们的和是10,求乙的得分是780分的情况下, 上述三项的比例的可能的值
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 85 | 90 |
| 面试 | 93 | 70 | 68 |
22.大陆相关部门于2005年8月1日起对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售。某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
| 每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
| 每天销量(千克) | 50 | 52 | 54 | 56 | … | 86 |
|
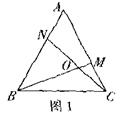
23.课外学习小组在一次学习研讨中,得到了如下两个命题:
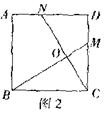
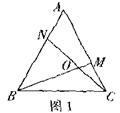
①如图1,在正三角形ABC中,M,N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°则BM=CN:
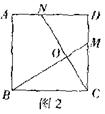
②如图2,在正方形ABCD中,M、N分别是CD、AD上的点.BM与CN相交于点O,若∠BON=90°则BM=CN.
然后运用类似的思想提出了如下命题:
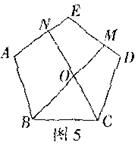
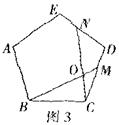
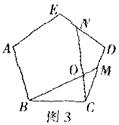 ③如图3.在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°则BM=CN.
③如图3.在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°则BM=CN.
任务要求
(1)请你从①.②,③三个命题中选择一个进行证明;
 (说明:选①做对的得5分,选②做对的得4分,选③做对的得6分)
(说明:选①做对的得5分,选②做对的得4分,选③做对的得6分)
(2) 请你继续完成下面的探索;
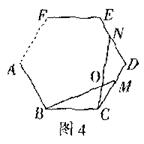
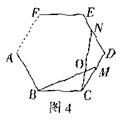
①如图4,在正n(n≧3)边形ABCDEF![]() 中,M,N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明)
中,M,N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明)
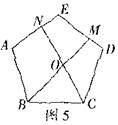
②如图5,在正五边形ABCDE中,M、N分别是DE,AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否还成立,若成立,请给予证明.若不成立,请说明理由
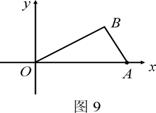
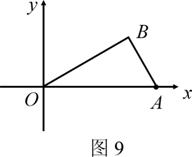
24如图,已知O为坐标原点,∠AOB=30°,∠ABO=90°,OA=2.
(1) 求点B的坐标;
![]() (2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
(2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由
|
 九年级数学阶段性测试卷(答卷)
九年级数学阶段性测试卷(答卷)
一、选择题:(每小题3分, 共30分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
|
|
|
|
|
|
|
|
|
|
二、填空题:(每小题4, 共24分)
11.________________, 12.____________________ 13.____________________________________
14.__________________ 15.______________________ 16.______________________________
三、解答题:(本题有8小题, 共66分)
17. (本题6分)(1)![]() (2)
(2)![]()
18. (本题6分)
计算(1) ![]() (2)
(2) ![]()
19. (本题 6分)
 20. (本题8分)
20. (本题8分)
21 (本题8分)
22. (本题 8分)
23. (本题12分)
 (1)我选
(1)我选
证明:
(2) ∠BON等于___________时,结论BM=CN成立
(3) 证明:
24. (本题12分)
![]()