九年级数学期末测试题（二）
时间：90分钟 分数：120分
一、选择题（每小题3分，共30分）
1．（2004·厦门）下列计算正确的是（ ）
（A）·＝ (B) ＋＝
(C) ＝3 (D) ÷＝2
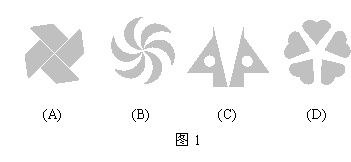2．（2004·淄博）在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转.下列图案中，不能由一个圆形通过旋转而构成的是（ ）
3．（2004·聊城）已知
，则
的值为（ ）
A．
B．
C．
D．
4．（2004·浙江嘉兴）已知圆锥的底面半径为3，高为4，则圆锥的侧面积为（ ）
（A）10π （B）12π （C）15π （D）20π
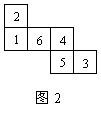
5．（2005·浙江)一个均匀的立方体六个面上分别标有数1，2，3，4，5，图2是这个立方体表面的展开图．抛掷这个立方体，则朝上一面上的数恰好等于朝下一面上的数的
的概率是（ ）
A、
B、
C、 D、
6．（2004·泰州）若代数式
的值是常数2,则a的取值范围是（
）
A.
≥4 B.≤2 C. 2≤a≤4 D. 
或
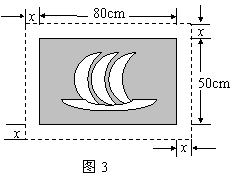7．（2004·陕西）在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图3所示，如果要使整个挂图的面积是5400cm2，设金色纸边的宽为xcm，那么x满足的方程是（ ）
A．x2+130x-1400=0
B．x2+65x-350=0
C．x2-130x-1400=0
D．x2-65x-350=0
8．（2004·淄博）若关于x的一元二次方程
有实数根，则k的取值范围是（ ）
（Ａ）k＞－1
（Ｂ）k≥－1
（Ｃ）k＞－1且k≠0 （Ｄ）k≥－1且k≠0
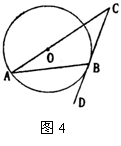
9．（2004·北京石景山）如图4，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）
（A）72° （B）63° （C）54° （D）36°
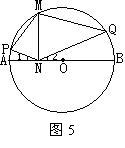10．（2004·福州）如图5，AB是⊙O的直径，M是⊙O上一点，MN⊥AB，垂足为N，P、Q分别是AM、BM上一点（不与端点重合），如果∠MNP=∠MNQ，下面结论：①∠1=∠2；②∠P+∠Q=∠180°；③∠Q=∠PMN；④PM=QM；⑤MN2=PN·QN。
其中正确的是（ ）
A．①②③ B．①③⑤ C．④⑤ D．①②⑤
二、填空题（每小题4分，共40分）
11．（2005·浙江）已知⊙O的半径为8, 圆心O到直线l的距离是6, 则直线l与⊙O的位置关系是 ．
12．（2005·梅列）在抛掷一枚普通正六面体骰子的过程中，出现点数为2的概率是 。
13．（2004·新疆）已知
，则
.
14．（2004·甘肃）方程
的根是
。
15．（2004·山西）实数a在数轴上的位置如图6所示，
化简：
。
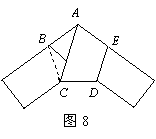16．（2004·淄博）用一条宽相等的足够长的纸条，打一个结，如图7所示，然后轻轻拉紧、压平就可以得到如图8所示的正五边形ＡＢＣＤＥ，其中∠ＢＡＣ＝ 度.
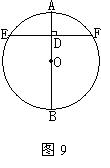
17．（2004·北京朝阳）已知：如图9，AB是⊙O的直径，弦EF⊥AB于点D，如果EF=8，AD=2，则⊙O半径的长是 。
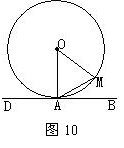
18．（2004·宁波）如图10，DB切⊙O于点A，∠AOM=66°，则∠DAM= 度。
 | |||
 |
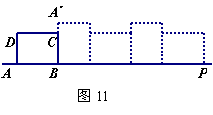19．（2004·温州）已知矩形ABCD的长AB=4,宽
AD=3,按如图11放置在直线AP上,然后不滑动地转动,
当它转动一周时( A →A′),顶点A所经过的路线长等
于 。
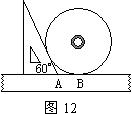20．（2004·锦州）如图12，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3.5cm，则此光盘的直径是_____cm.
三、解答题
21．（6分）（2004·北京丰台）计算：
。
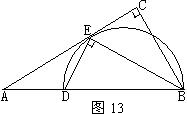22．（8分）（ 2004·广东）如图13，在Rt△ABC中，
,BE平分∠ABC交AC于点E，点D在AB上，
.
（１） 求证：AC是△BDE的外接圆的切线；
（２）若
，求EC的长.
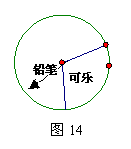23．（12分）（2004·温州）某商场设立了一个可以自由转动的转盘,并规定：顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据：
(1) 计算并完成表格：
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 |
|
|
|
|
|
|
(2) 请估计,当n很大时,频率将会接近多少？
(3) 假如你去转动该转盘一次,你获得铅笔的概率约是多少？
(4) 在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少(精确到1°)
24．（12分）（2004·北京英才苑）如图15，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆。
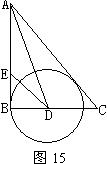求证：（1）AC是⊙D的切线；（2）AB+EB=AC。
四、应用题
25．（12分）（2004·彬州）今年，我国政府为减轻农民负担，决定在5年内免去农业税.某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同.
（1）求降低的百分率；
（2）若小红家有4人，明年小红家减少多少农业税？
（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税.
期末测试题（二）
一、选择题
1．A 2．C 3．A 4．C 5．A 6．C 7．B 8．D 9．B 10．D
二、填空题
11．相交
12．
13．20 14．
15．1 16．36 17．5
18．147 19．
20．
三、解答题
21．—2
22．解：（1）取BD的中点O，连接OE。
∵BE平分∠ABC，∴∠CBE=∠OBE。又∵OB=OE，∴∠OBE=∠BEO，∴∠CBE=∠BEO，∴BC∥OE。∵∠C=90°，∴OE⊥AC，∴AC是△BDE的外接圆的切线。
（2）设⊙O的半径为r，则在△AOE中，
，即
，解得
,
∴OA=2OE，
∴∠A=30°，∠AOE=60°。
∴∠CBE=∠OBE=30°。
∴EC=
。
23．解：（1）
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
（2）当n很大时,频率将会接近0.7；
（3）获得铅笔的概率约是0.7；
（4）扇形的圆心角约是
。
24．证明：（1）过点D作DF⊥AC于F.
∵AB为⊙D的切线, AD平分∠BAC, ∴BD=DF .
∴AC为⊙D的切线 .
（2）在△BDE和△DCF中, ∵BD=DF, DE=DC,
∴△BDE≌△DCF（HL）, ∴EB=FC .
又AB=AF, ∴AB+EB=AF+FC, 即AB+EB=AC .
四、应用题
25．（1）设降低的百分率为x，
依题意有 
，解得x1＝0.2＝20％，x2 ＝1.8(舍去)；
（2）小红全家少上缴税 25×20％×4＝20（元）；
（3）全乡少上缴税 16000×25×20％＝80000（元）。
答略。