九年级数学期末考试模拟试题(六)
班级_______ 学号________ 姓名________ 成绩________
一、精心选一选(本大题共有8小题，每小题3分，共24分．)
1．有理式
，-
，
，
，-
a-9b，
-
中分式共有（ ）个．
A．5 B．4 C．3 D．2毛
2、某型号的手机连续两次降价,其售价由原来的1185元降到了580元.设平均每次降价的百分率为x,则列出的方程正确的是（ ）
A、580（1+X）
=1185
B、1185（1+X）=580
C、580（1-X）=1185
D、1185（1﹣X）=580
3．如果关于x的一元二次方程x2-x+m=0有两个不相等的实数根且两根之差的平方小于1，那么实数m的取值范围是（ ）．
A．m>0 B．m≤
C．0<m≤
D．0<m<
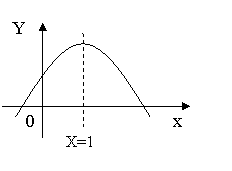
4、已知二次函数y=ax
+bx+c的图像如图所示，对称轴是x=1，则下列结论正确的是 ( )
A，ac＞0 B, b＜0
C, b-4ac＜0 D,
2a+b=0
5、⊙O的直径为12㎝，弦AB垂直平分半径OC，则弦AB的长为（ ）
A、3
㎝ B、6㎝
C、6㎝ D、12㎝
6、甲、乙两人投掷两个普通的正方体骰子，规定掷出“和为7”算甲赢，掷出“和为8”算乙赢，这个游戏是否公平？
( )
A．公平 B.对甲有利 C、对乙有利 D、无法判断
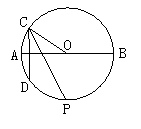
7．如图，AB为⊙O的一固定直径，它把⊙O分成上下两个半圆，自上半圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在上半圆（不包括A，B两点）上移动时，点P（ ）．
A．位置不变; B．到CD的距离保持不变;
C．等分弧BD; D．随点C的移动而移动
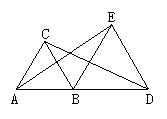
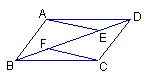
8．如图1，△ABC与△BDE都是等边三角形，AB<BD，若△ABC不动将△BDE绕B点旋转，则在旋转过程中AE与CD的大小关系（ ）．
A．AE=CD B．AE>CD C．AE<CD D．无法确定
二、细心填一填(本大题共有8小题，每小题3分，共24分．)
9、生物学家发现一种病毒的直径约为0.m,用科学计数法记为
。
10、如图，平行四边形ABCD中，BD是对角线，E、F是对角线上的点，
要使△BCF≌△DAE，还需添加一个条件（只需一个条件）是 。
11．如果关于x的方程
+3=
有增根，那么增根是________．
12. 二次函数
的最小值是_____________。
13．α，β是方程x2+2x-5=0的两根，则α2+αβ+2α=________．
14.已知两圆内切，圆心距为3㎝，如果一圆的半径是5㎝，则另一圆的半径是 ㎝。
15．两个三角形如果具有条件：（1）三条边对应相等；（2）两条边和夹角对应相等；（3）两条边和其中一边的对角相等；（4）三个角对应相等。
那么一定能判断两个三角形全等的条件是 （填序号）。
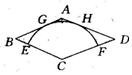16．如图，在菱形ABCD中，∠A=35°，AB=
，以点C为圆心的弧EF分别与AB，AD相切于点G，H，与BC，CD分别相交于点E，F用
扇形CEF做成圆锥的侧面，则圆锥的高为___________．
三、认真答一答(本大题共有9小题，共52分。)
17、（本题共8分）（1）计算：+2（3.14-π）0-（-1）-2003+
（2）解方程：
-
=
18. （本题共4分）先化简，在选取一个使分式有意义,而你又喜欢的数代入求值：
（
-
）÷
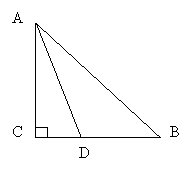
19. （本题共5分）如图，在Rt△ABC中，∠C＝90°，BC＝AC，AD平分∠BAC交BC于D，求证：AB＝AC＋CD
 |
20．（本题共4分）袋中共有5个大小相同的红球、白球，任意摸出一球为红球的概率是
。
（1）袋中红球、白球各有几个？
（2）任意摸出两个球均为红球的概率是多少？
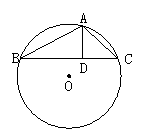
21．（本题共5分）如图，△ABC内接于⊙O，AB+AC=12，AD⊥BC于D，AD=3，设⊙O的半径为y，AB的长为x，试用含有x的代数式表示y．
22． （本题共5分）AB为⊙O的直径，把AB分成几条相等的线段．
以每条线段为直径画小圆，设AB=a，那么⊙O的周长为L=
a，计算：
（1）把AB分成两条相等的线段，每个小圆的周长L2=
a=L．
（2）把AB分成三条相等的线段，每个小圆的周长L3=________．
（3）把AB分成四条相等的线段，每个小圆的周长L4=________．
……
（4）把AB分成n条相等的线段，每个小圆的周长Ln=_______．
结论：把大圆的直径分成n条相等的线段，以每条线段为直径分别画小圆，那么每个小圆周长是大圆周长的_______．
23. （本题共5分）已知下列n（n为正整数）个关于x的一元二次方程：
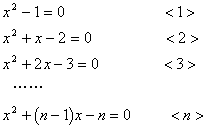
（1）请解上述一元二次方程<1>、<2>、<3>、<n>；
（2）请你指出这n个方程的根具有什么共同特点，写出一条即可。
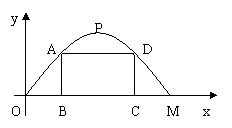
24、（本题共8分）某施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米，现以点O为原点，OM所在直线为x轴建立直角坐标系（如图所示），
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数关系式；
（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D 点在抛物线上，B、C点在地面OM上，为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少，请你帮施工队计算一下。
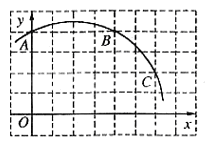
25. （本题共8分）如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C。
（1）用直尺画出该圆弧所在圆的圆心M的位置；
（2）若A点的坐标为（0，4），D点的坐标为（7，0），试验证点D是否在经过点A、B、C的抛物线上；
（3）在（2）的条件下，求证直线CD是⊙M的切线。
