九年级数学期中试卷
班级：_________ 姓名：_________ 学号：_________ 得分：_________
一、选择题。（本题有12个小题，每小题4分，共48分）
1.反比例函数
的图象位于
(
)
A、第一、二象限 B、第一、三象限 C、第二、三象限 D 、第二、四象限
2.若反比例函数
经过点A(m,-2m),则m的值为( )
A、
B、3
C、±
D、±3
3. 抛物线
的对称轴是（ ）
A. 直线
B. 直线
C. 直线
D. 直线
4．抛物线y= -
（x+1）2+3的顶点坐标（ ）
A（1，3） B（1，-3） C（-1，-3） D（-1，3）
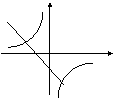
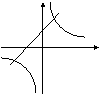
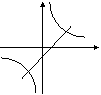
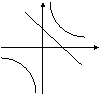
5、在同一坐标系中，函数
和
的图象大致是 （ ）
 | |||||||
 |  |  | |||||
A B C D
6．函数
的图象与
轴有交点，则
的取值范围是（ ）
A．
B．
C．
D．
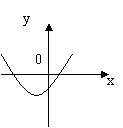7、二次函数
图象如图所示,下面结论正确的是 ( )
A、 
＜0,
＜0,
＞
B、 ＞0,＜0,＞
|
＞0,＞0,＞ D、＞0,＜0,＜
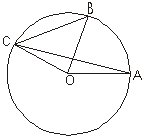
8、AB为50度，∠OBC＝40°，则∠OAC＝ ( )
A、15° B、20° C、25° D、30°
9．抛物线
与x轴交点的个数是（ ）
A.0个 B.1个 C.2个 D.以上答案都不对
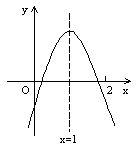
10. 二次函数
的图像，如图所示，下列结论：①
，②
，③
，④
<０其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
|
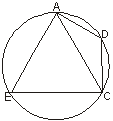
11、△ABC是圆内接正三角形，AD的度数为60°，则△ADC与△ABC的面积之比为 ( )
A、5/8 B、3/5 C、2/3 D、1/3
12．二次函数的最大值是0，则 a+
化简的结果是（ ）
A. a B. －c C. 1 D. 0
二、填空题。（本题有6个小题，每小题5分，共30分）
13．如果一个反比例函数y=
的图象经过点（2，-3），则k的值是_________．
14．某抛物线与X轴的交点的横坐标为-3和7，则对称轴为直线_________．
15．把一个半径为8cm的圆，剪去一个圆心角为90°的扇形后，剩下的部分做成一个圆锥的侧面，那么这个圆锥的高为 _________cm．
16. 如图，AB是⊙O的一条弦，P是AB上的一点，
，则⊙O的半径等于__________。
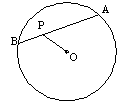（第１６题） 
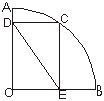（第１７题）
17．如图，半径OA垂直OB，C是弧AB上一点，CD垂直OA于D，CE垂直OB于E，若OD＝5，AD＝2，则DE＝________
18．把抛物线y=3x2先向上平移2个单位，再向右平移3个单位，所得抛物线的解析式是 .
|
|
19、如图，AB是⊙O的直径，且AD∥OC，若AD的度数为80°。求 CD的度数。（8分）
20、（8分）你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y (m)是面条的粗细(橫截面积)s(㎜2)的反比例函数，其图象如图所示。
(1)写出y与s的函数关系式；
(2)求当面条粗1.6㎜2时，面条的总长度是多少？
21. （8分）如图，用长为18 m的篱笆（虚线部分），两面靠墙围成矩形的苗圃。
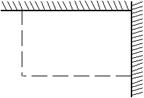（1）设矩形的一边为
（m），面积为
(m2)，求关于的函关系式，并写出自变量的取值范围；
（2）当为何值时，所围苗圃的面积最大，最大面积是多少？
22、(10分)AB、CD为⊙O内两条相交的弦，交点为E，且AB=CD。则以下结论中：①AE=EC、②AD=BC、③BE=EC、④AD∥BC，正确的有 。试证明你的结论。
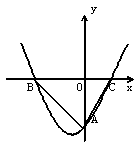
23、（12分）二次函数
的图像与轴交于B，C两点，与y轴交于A点。
（1）、根据图像确定a，b，c的符号，并说明理由；
（2）、如果点A的坐标为（0，－3），∠ABC=45°, ∠ACB=60°,求这个二次函数的解析式。
24、(12分)如图，二次函数y=ax2+bx+c(a≠0)的图像与x轴交于A、B两点，其中点A坐标为(―l，0)，点C(0，5)，D(1，8)在抛物线上，M为抛物线的顶点。
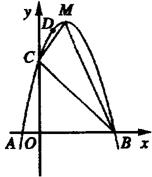(1)求抛物线的解析式；
(2)求抛物线顶点M的坐标和B点的坐标。
(3)求△MCB的面积。
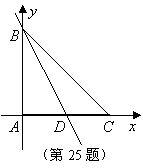
25．（本小题满分14分）
已知
，
是
边上的中线，分别以
所在直线为轴，
轴建立直角坐标系（如图）．
（1）在
所在直线上找出一点
，使四边形
为平行四边形，画出这个平行四边形，并简要叙述其过程；
（2）求直线的函数关系式；
（3）直线上找一点
，使
为等腰三角形，求点的坐标（至少找到两个点）。
 |