九年级数学秋学期期末模拟练习一
一、选择题（每题3分，计36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、直角三角形的两边长分别是6，8，则第三边的长为（ ）
A．10 B．2
C．10或2
D．无法确定
2、以等腰三角形顶角的顶点为圆心，顶角平分线为半径的圆，必与底边（ ）
A. 相离 B. 相交 C. 相切 D. 无法确定
3、下列函数的图象中，有最高点的函数是（ ）
A．y＝3x＋5 B．y＝－2x＋3 C．y＝
x2 D．y=－4x2
4、化简二次根式
的结果是（ ）
A．
B． 
C．
D．
5、已知关于ｘ的一元二次方程ｘ２－2(Ｒ＋ｒ)ｘ＋ｄ２＝０有实数根，其中Ｒ、ｒ分别为
⊙Ｏ１、⊙Ｏ２的半径，ｄ为两圆的圆心距，则⊙Ｏ１与⊙Ｏ２的位置关系是 (
)
Ａ．外离 Ｂ．相交 Ｃ．相切 Ｄ．以上都不正确
6、已知三角形的外心在三角形的外部，那么这个三角形是 （ ）
A. 任意三角形 B. 直角三角形 C. 锐角三角形 D.钝角三角形
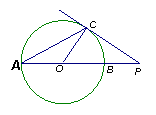7、一个点与定圆上最近点的距离为4cm，最远点的距离为9cm,则此圆的半径为 （ ）
A. 2.5cm B. 6.5cm C. 13cm或5cm D. 2.5cm或6.5cm
8、已知⊙0的直径AB与弦AC的夹角为35°，
过C点的切线PC与AB的延长线交于点P，则么P等于（ ）
A．15° B．20° C．25° D．30°
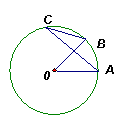
9、如图，OA、OB是⊙O的半径，∠O＝40°，∠B＝50°，
则∠A等于（ ）
A、80° B、70° C、60° D、30°
10、 两圆既不相交又不相切，半径分别为3和5，则两圆的圆心距d的取值范围是（ ）
A．d＞8 B．0＜d≤2 C．2＜d＜8 D．0≤d＜2或d＞8
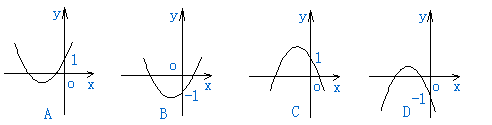11、如图，如果函数
的图象在第一、二、三象限，那么函数
的图象大致是（ ）
12、如图，四边形ABCD为圆内接四边形，E为DA延长线上一点，若︵BAD的度数为70°，则∠BAE的度数为 （ ）
A．140° B．70° C．35° D．20°
二、填空题（每题3分，计30分）
13、Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，则它的外心与顶点C的距离为 cm。
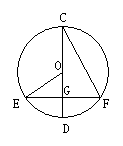14、如图，⊙O的直径CD过弦EF的中点G，∠EOD=40°,则∠DCF= °。
15、当
＝ 时，函数y＝（
）
是二次函数．
16、若化简
的结果为
,
则
的取值范围是 。
17、数据－1，1，0，
的平均数为0，则这组数据的方差为
。
18、如果抛物线
的顶点到轴的距离是3,那么c的值为 。
19、一组数据2、5、6、
的极差是7，则的值为___ ____．
20、已知圆锥的侧面展开图的图心角是72°，它的侧面积为10πcm2，则该圆锥的全面积
是 cm2.
21、已知点P是半径为5的⊙Ο内一定点，且PO=4，则过点P的所有弦中，弦长可取到的整数值共有的条数是
22、若⊙O1和⊙O2相交于A、B两点，⊙O1和⊙O2的半径分别为2和
，公共弦长为2，∠O1AO2的度数为
三、解答题：
21、（1）计算：（6分） （2）解方程：（6分）
22、（12分）已知
是二次函数，且函数图象有最高点。
（1）求k的值；（2）求顶点坐标和对称轴．
23、（12分）已知：如图，在△ABC中，AB=AC，以AB为直径的圆交BC于D，过D作DE⊥AC于E。
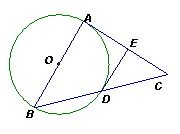求证：DE是⊙O的切线
24、（12分）利达经销店为某工厂代销的一种建筑材料，当每吨售价为260元时，月销售量为45吨，该经销售店为提高经营利润，准备采取降价的方式进行促销。经市场调查：当每吨售价每下降10元时，月销售量就会增加7.5吨。综合各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元，设每吨材料售价为x（元），该经销店的月利润为y（元）。
1）、求出y与x之间的函数关系式。（不要求写出x的取值范围）。
2）、该经销店要获得最大月利润，售价应定为每吨多少元？
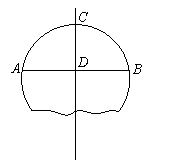25、(12分)
如图，破残的圆形轮片上，弦AB的垂直平分线交AB于C，交弦AB于D.
(1)求作此残片所在的圆(不写作法，保留作图痕迹)；
(2)若AB＝24cm，CD＝8cm，求(1)中所作圆的半径.
26、（12分）△ABC 外切于⊙O ，切点分别为点D、E、F，∠A＝600，BC＝7,⊙O的半径为
．
⑴求BF+CE的值
⑵求△ABC的周长．
27、 (本题满分12分)
有一座抛物线形拱桥，正常水位时桥下水面宽度为20m，拱顶距离水面4m.
⑴ 在如图所示的直角坐标系中，求出该抛物线的解析式；
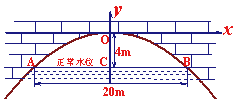⑵ 设正常水位时桥下的水深为2m，为保证过往船只顺利航行，桥下水面的宽度不得小于18m，求水深超过多少米时就会影响过往船只在桥下的顺利航行.