九年级第二学期期中数学试卷

九年级第二学期期中数学试卷

班级　　　 姓名　　　　座号 　　　　　　 

温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！

参考公式：① 二次函数y=ax²+bx+c图象的顶点坐标是；

② 圆锥的侧面积是πrl，其中r是圆锥底面圆的半径，l是圆锥的母线长．

一、选择题（本题有12小题，每小题4分，共48分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1．据2006年10月2日《温州日报》报道，“十一”黄金周期间2006年10月1日楠溪江的游客接待量累计176000人次．用科学记数法表示为（　　）

Ａ．人次　　　　　　　　　　　　　　　　　　　　　　 Ｂ．人次　　

Ｃ．人次　　　　　　　　　　　　　　　　　　　Ｄ．人次

2. 如图１所示，圆柱的俯视图是（　　）

图１　　　 　　（Ａ）　　　　　（Ｂ）　　　　 （Ｃ）　　　　（Ｄ）

3. 数据1，2，3，3，4，5的中位数是（　　）.

　　(A) 2　　(B) 3　　 (C) 4　　　(D) 5

4. 下列y关于x的函数中，属于二次函数的是（　　 ）

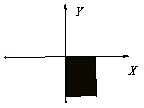A 　　 B 　　　C 　　D

5. 在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，

则目标的坐标可能是（　　　）

A、（-3,300） B、（7,-500） C、(9,600)　　D、(-2,-800)

6．已知一点和圆心的距离为3，圆的半径分别为4，那么这点和圆位置关系是（　　）

A．圆上　　　　　　　 B．圆外　　　　　　　　C．圆内　　　　　　　 D．不能确定

7． 如图，A，B，C是⊙O上的三点，∠BAC= 45°，

则∠BOC的大小是（　　）

A．90°　　　　　　　 B．60°　　　　　　　　

C．45°　　　　　　　 D．22.5°

8． 小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能是（　　）

9．如果两点P₁(1，y₁)和P₂(2，y₂)在反比例函数的图象上，那么（　　）

A．y₂＜y₁＜0　　　　B．y₁＜y₂＜0　　　　C．y₂＞y₁＞0　　　　D．y₁＞y₂＞0

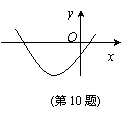
10．抛物线y=ax²+bx+c的图象如右, 则 (　 )

A. a<0　　　　　　　　 B. b<0

C. b²-4ac<0　　　　　　 D. c<0

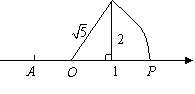11．“数轴上的点并不都表示有理数，如图中数轴上的点所表示的数是”，这种利用图形直观说明问题的方式体现的数学思想方法叫（　　）

Ａ．代入法

Ｂ．换元法

Ｃ．数形结合的思想方法

Ｄ．分类讨论的思想方法

12．自2006年3月26日起，国家对石油开采企业销售国产石油因价格超过一定水平（每桶40美元）所获得的超额收入，将按比例征收石油特别收益金（征收比率及算法举例如下面的图和表）．有人预测中国石油公司2006年第3季度将销售200百万桶石油，售价为每桶53美元，那么中国石油公司该季度估算的特别收益金将达到人民币（按1美元兑换8元人民币的汇率计算）（　　）

A．62.4亿元　　　　B．58.4亿元　　　　 C．50.4亿元　　　　D．0.504亿元

二、填空题（本题有6小题，每小题5分，共30分）

13．有关部门需要了解一批食品的质量情况，通常采用的调查方式是　　　（填：抽样调查或普查）．

14．已知反比例函数，当x=2时，y= -4，该函数关系式是　　　　  .．

15．二次函数y=(x－2)²－1的顶点坐标为　　　　　   ．

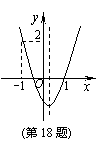
16．一个函数的图象经过点（1，2），且y随x的增大而增大而这个函数的解析式是（只需写一个）　　　 _　　　　　　　　　　　 _。

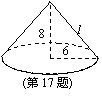
17．如图，圆锥的底面半径为6cm，高为8cm，

那么这个圆锥的侧面积是　　　 cm²．

18．如图，二次函数的图象开口向上，

图象经过点（-1，2）和（1，0），且与轴相交于负半轴．

(以下有(1)、(2)两问，每个考生只须选答一问，若两问都答，则只以第(2)问计分)

第(1)问：给出四个结论：① ；② ；③ ；

④ ．其中正确结论的序号是　　　（答对得3分，少选、错选均不得分）．

第(2)问：给出四个结论：① ；② ；③ ；④．其中正确结论的序号是　　　（答对得5分，少选、错选均不得分）．

三、解答题（共72分）

19（本题12分）

(3－π)⁰　　　　　　　　 解方程：2x²－9 x=5

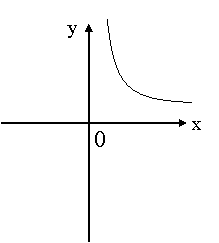20（本题6分） 已知反比例函数的图象的一个分支如图，

请补画它的另一个分支，

（不写画法，但必须保留痕迹）

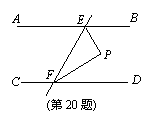20．（本题8分）已知：如图，直线AB∥CD，直线EF分别交AB，CD于点E，F，∠BEF的平分线与∠DFE的平分线相交于点P．

求证：∠P=90°．

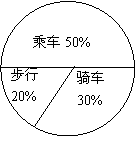
21.（本题12分）下图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。

　　（1）求该班有多少名学生？

　　（2）补上步行分布直方图的空缺部分；

　　（3）在扇形统计图中，求骑车人数所占的圆心角度数。

　　（4）若全年级有500人，估计该年级步行人数。

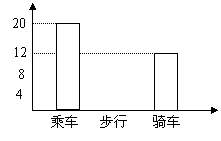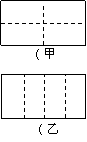
22（本题12分）现有一张长和宽之比为2∶1的长方形纸片，将它折两次（第一次折后也可打开铺平再折第二次），使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作)，如图甲（虚线表示折痕）. 除图甲外，请你再给出三个不同的操作，分别将折痕画在图①至图③中 (规定:一个操作得到的四个图形，和另一个操作得到的四个图形，如果能够“配对”得到四组全等的图形，那么就认为是相同的操作．如图乙和图甲是相同的操作) ．

23．（本题10分）如图，已知AB为⊙O的直径，AC为弦，OD∥BC交AC于D，OD =，求BC的长；

24.（本题12分）已知二次函数的图象经过点A（2，0）且与直线相交于B、C两点，点B在轴上，点C在轴上；

（1）　　求二次函数的解析式；

（2）　　如果P（，）是线段BC上的动点，O为坐标原点，试求ΔPOA的面积与之间的函数关系式，并求自变量取值范围；

（3）　　在（2）的条件下，是否存在这样的点P，使ΔPOA为等腰三角形？若存在，求出P点的坐标;若不存在，请说明理由.