九年级第一学期第一次月质量检测数学试卷
（时间：120分钟 总分：150分）
（第一卷不用交，只交第二卷）
嗨！你们好，进入初三后，学习是不是很辛苦？不过，只要紧一紧，谁都能行！如果松一松，什么都会落空。俗话说，书山无路勤为径！同学们，在你答卷之前，请认真审题，只要你理解概念，仔细运算，积极思考，相信你会成功的，会考出理想的数学成绩的！加油哦。
一，选择题（请把正确选项写在答案卷上，每题3分，共计30分）
1. 式子
在实数范围内有意义，则
的取值范围是
（A）
≥
（B）
（C）≤1 （D）≥1
2. 关于的方程
是一元二次方程，则
（A）
（B）
（C）
（D）≥0
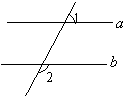3. 如图，直线∥
，
，则∠2的度数是
（A）
（B）
（C）
（D）
4. 下列计算过程正确的是
（A）
（B）
（C）
（D）
5 .如图， ABCD中，
，则
的度数是
（A）50° （B）60° （C）70° （D）80°
6. 用配方法解下列方程，其中应在左右两边同时加上4的是
（A）
（B）
（C）
（D）
7. 边长为
的等边三角形的面积是
（A）6 （B）
（C）
（D）3
8. 对于方程
的根的情况，下列说法中正确的是
（A）方程有两个不相等的实数根 （B）方程有两个相等的实数根
（C）方程没有实数根 （D）方程只有一个实数根
9. 一个等腰三角形的一边长为1，另一边长为
，则这个等腰三角形的周长等于是
（A）
（B）
（C）
（D） 或
10. 有一人患了流感，每轮传染中平均一个人传染了个人，则经过两轮传染后，患流感的总人数用含的代数式表示是
（A）
（B）
（C）
（D）
二，填空题（请把正确答案写在答案卷上，每题4分，共计20分）
11. 方程
的根是
。
12. 反比例函数
的图像经过点（
，
），则
的值等于
。
13. 已知
是方程
的一个根，代数式
的值是 。
14. 当
，分式
的值是
。
15. 如图，在平面直角坐标系中，
，
，
是三角形的三个顶点，则
的长是
。
三，解答题（请把正确答案写在答案卷上，共计100分）
16. 计算：（每小题6分，共计12分）
（1）
（2）
17. 解方程：（每小题6分，共计12分）
（1）
（2）
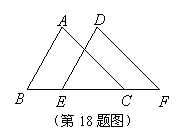18.（本题12分）
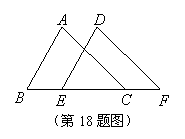
已知：如图，
，
，
. 求证：
.
19.（本题12分）
已知
，
，求代数式
的值。
20.（本题12分）
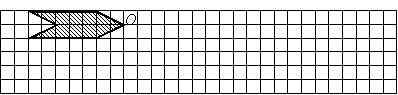
将下图中的阴影部分向右平移6个单位后，再向下平移4个单位，点O落在点
处。
（1）画出经两次平移后的阴影部分图案；
（2）求
的长度。
 |
21.（本题12分）
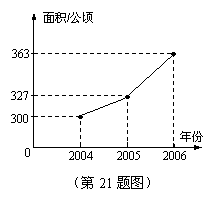
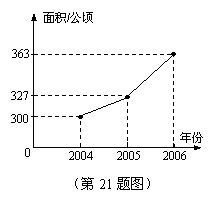近年来，市政府不断加大对城市绿化的经济投入，使全市绿地面积不断增加，从2004年底到2006年底，城市绿地面积变
化如图所示。
（1）根据统计图，从2004年底到2006年
底，绿化面积增长最多的一年是 年，
该年的绿化面积比前一年增长了 公顷；
（2）求绿地面积的年平均增长率。
22.（本题13分）
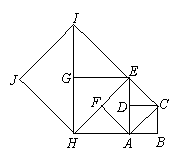
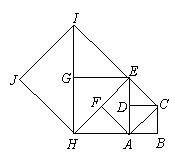
如图，设正方形
的边长为1，以正方形的对角线
为边作正方形
，再以第二个正方形的对角线
为边作第三个正方形
，如此下去…，解答下列问题：
（1）记正方形的边长为
，依上述方法所作的正方形的边长依次为
，
，
，…，
，求出，，的值。
|
个正方形的边长的表达式。
（３）多边形
的面积等于 。
23.（本题15分）
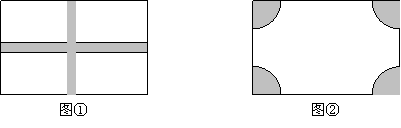
将一块长18米，宽15米的矩形荒地修建成一个花园（阴影部分），所占的面积为原来荒地面积的三分之二. （精确到0.1米）
（1）设计方案1（如图①）花园中修两条互相垂直且宽度相等的小路；
（2）设计方案2（如图②）花园中每个角的扇形都相同。
 |
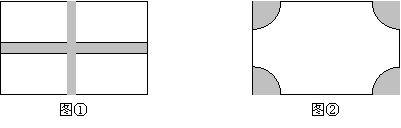以上两种方案是否都能符合条件？若能，请计算出图①中小路的宽和图②中扇形的半径；若不能符合条件，请说明理由。
四，附加题（此题只给以上得分少于90分的同学，但最多不超过90分）
1，（本题5分）任意写出一个二次根式；
2，（本题5分）写出一元二次方程
的求根公式。
第一学期九年级第一次月考
数学试卷答案卷
（时间：120分钟 总分：150分）
| 题号 | 一 | 二 | 三 | 总得分 | |||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | ||||
| 得分 | |||||||||||
一，选择题（每题3分，共计30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二，填空题（每题4分，共计20分）
11. ； 12. ；13. ；14. ；15. .
三，解答题（共计100分）
16. 计算：（每小题6分，共计12分）
（1）解： （2）解：
17. 解方程：（每小题6分，共计12分）
（1）解： （2）解：
18.（本题12分）
证明：
19.（本题12分）
解：
20.（本题12分）
（1）
（2）解：
21.（本题12分）
（1） 年； 公顷。
（2）解：
22.
（本题13分）
解：（１）
|
（２）
（３）多边形的面积等于 （直接写出答案）。
23.（本题15分）
设计方案１ 设计方案２
解：（１）设计方案１ ，设计方案２ 。（填
“符合”或“不符合”）
（２）以下供计算或说明理由。
四，附加题（此题只给以上得分少于90分的同学，但最多不超过90分）
1，（本题5分）你所写的二次根式是 ；
2，（本题5分）求根公式是 。